标签：
原文地址：http://www.researchgate.net/profile/Robert_Jacobs9/publication/223108796_Increased_rates_of_convergence_through_learning_rate_adaptation/links/0deec525d8f8dd5ade000000.pdf
已经看了CNN，rbm，sae等网络及算法，所有网络在训练时都需要一个learning rate，一直以来都觉得这个量设为定值即可，现在才发现其实这个量也可以变更和学习。
文章中提到的时最早的神经网络learning rate，不过我觉得对现在有启发作用。文中提出神经网络中，如果把error function看成是一个多变量函数，每个参数对应一个变量，那么这个函数在每个参数wi方向上变化的速度是不同的，并且如果error function不是圆形的话，负梯度方向并不是指向最小值的（这个画个椭圆做个切线就知道），因此应该采用不同的learning rate。
随后提出了作者一种启发式的方法就是在神经网络中，如果一个参数每次的导数的符号保持不变，说明它一直沿正方向走，那么应该增大learning rate以达到更快地到达最小值点，如果一个参数每次的导数的符号经常变化，说明它已经越过了最小值点，在最小值点附近摆动，那么应该减小learning rate让它稳定。
随后就是算法，一个是momentum方法，
，这样前面的导数可以影响后面的参数变更，从而使一直沿一个方向走的参数的改变，否则减小参数的改变。
第二种是delta-delta learning rule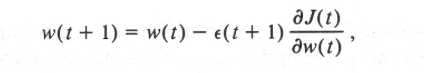
，这个ε(t＋1）是根据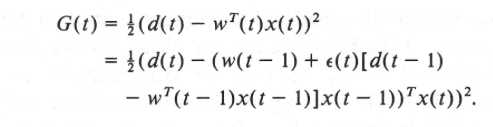
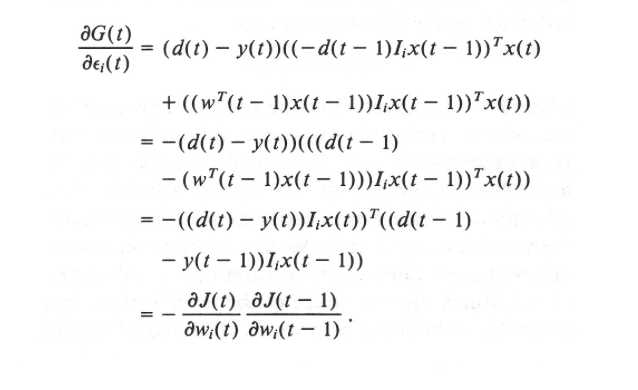
得出的，第二个式子的结果就是learning rate的导数，可以用sgd更新learning rate。但显然，这会有一个缺陷，结束第二个式子的结果是两个导数相乘，会比较小，所以这个方法不好，有个改进版的。
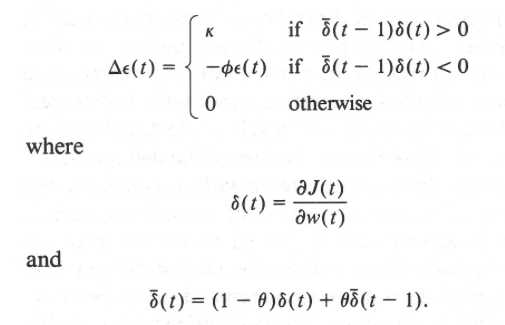
这个函数结合了那两个原则并且防止learning rate减到小于0，线性增加也不会增加的太快。
希望本博客对别人有帮助，谢谢。
关于Increased rates of convergence through learning rate adaptation一文的理解
标签：
原文地址：http://www.cnblogs.com/caozj/p/4841344.html
