第一章：数制和码制

标签：

数制

一、 十进制

进位规则是“逢十进一”。任意一个n位整数、m位小数的十进制可表示为：

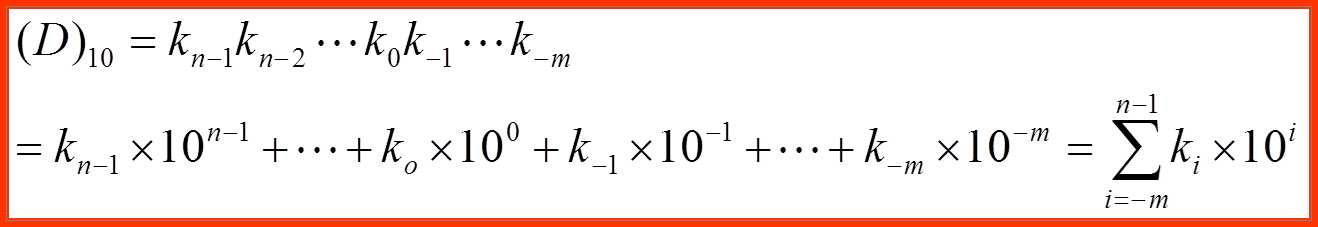
其中

k_i－称为数制的系数，表示第i位的系数，十进制ki的取值为0 ~ 9十个数， i 取值从 （n－1）～0的所有正整数到－1～－m的所有负整数

10ⁱ－表示第i位的权值，10为基数，即采用数码的个数

n、m－为正整数， n为整数部分的位数， m为小数部分的位数

例如

(249.56)10＝2×10²＋ 4×10¹＋ 9×10⁰+ 5×10^–1＋ 2×10^－2

二、 二进制

进位规则是“逢二进一”，任意一个n位整数、m位小数的二进制可表示为

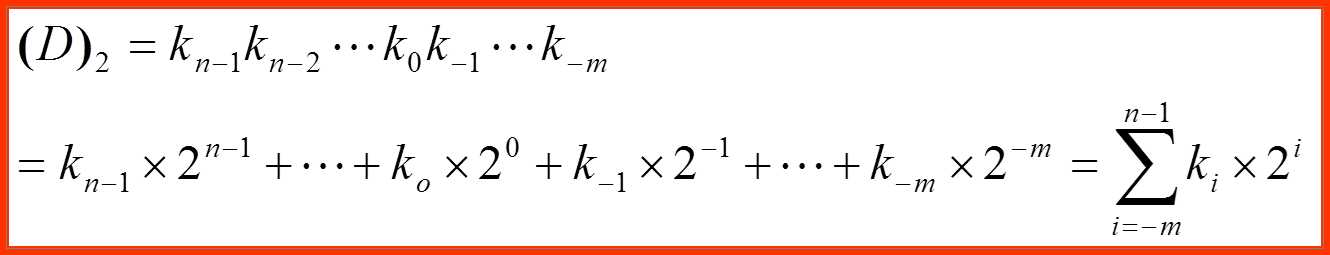
其中

k_i－取值只有两个数码：0和1

2ⁱ－为二进制的权，基数为2      

n、m－为正整数

如（11011.101)2=1×2⁴ +1×2³ +0×2² +1×2¹ +1×2⁰ +1×2^－1+0×2^-2 +1×2^－3=（27.625)₁₀

三、八进制

进位规则是“逢八进一”，其基数为8。任意一个n位整数、m位小数的八进制可表示为

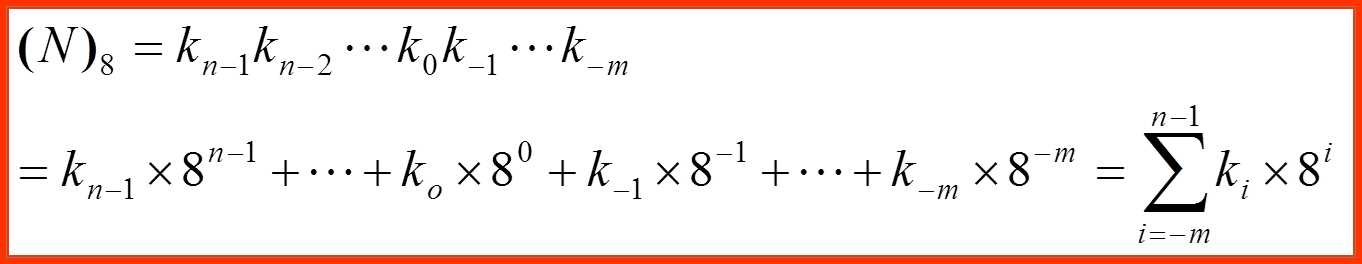
其中

k_i－取值有8个数码：0～7

8ⁱ－为八进制的权，基数为8                           

n、m－为正整数

如（13.74)8=1×8¹+3×8⁰ +7×8^－1+4×8^-2 =（11.9375)10

四、十六进制

进位规则是“逢十六进一”，其基数为16。任意一个n位整数、m位小数的十六进制可表示为

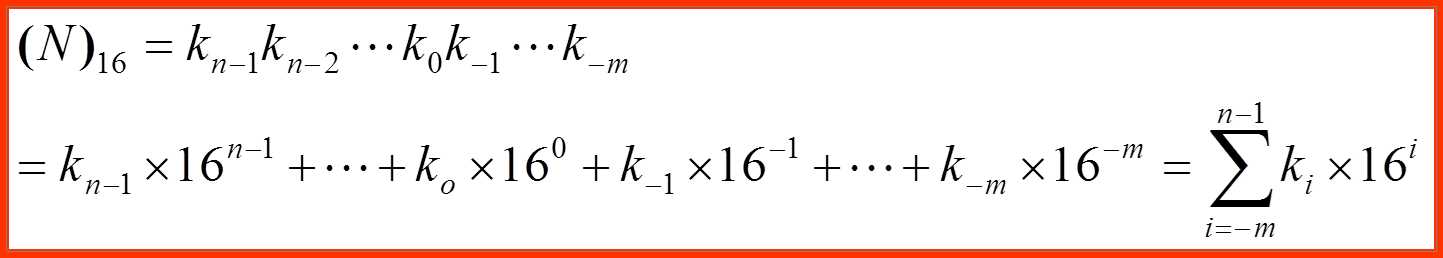
其中

k_i－取值有16个数码：0～9、A（10）、 B（11）、C（12）、D（13）、E（14）、 F（15）

16 i－为十六进制的权，基数为16                          

n、m－为正整数

（F9.1A)16=15×16¹+9×16⁰ +1×16^－1+10×16^-2 = （249.1015625)10

一个数码的进制表示，可用下标，如（N）2表示二进制； （N）10表示十进制； （N）8表示八进制， （N）16表示十六进制

有时也用字母做下标，如（N）B表示二进制，B－Binary；（N）D表示十进制，D－Decimal；（N）O表示八进制，O－Octal；（N）H 表示十六进制，H－Hexadecimal；

下表为0～15个数码的不同进制表示

不同数制间的转换

数制转换：不同进制的数码之间的转换叫做数制转换

一、 二进制数、八进制数和十六进制数转换成十进制数

        即将二进制数、八进制数和十六进制数转换成十进制数，方法是将二进制数、八进制数和十六进制数按下列公式进行展开即可

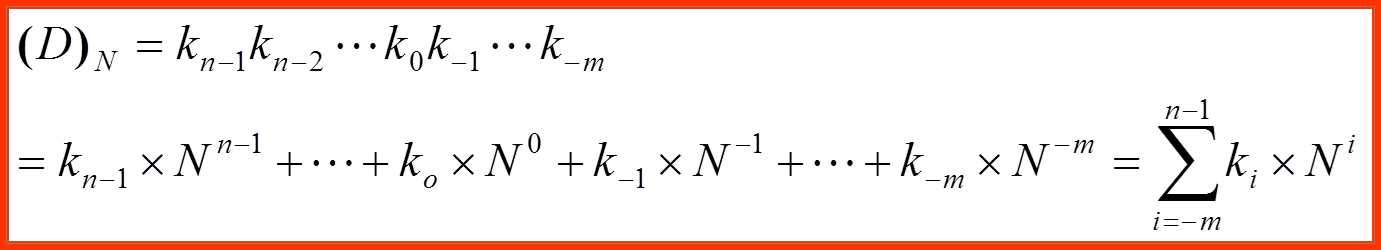
例如：

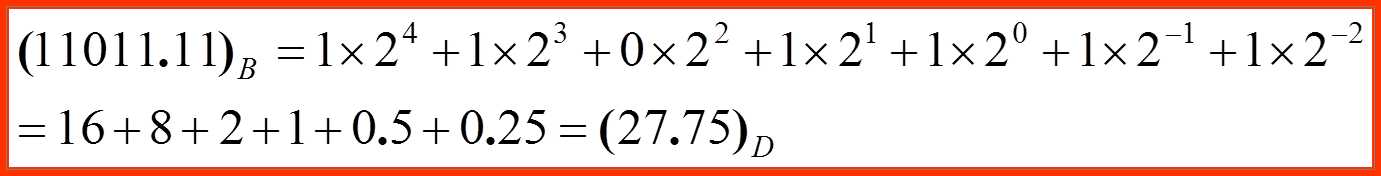
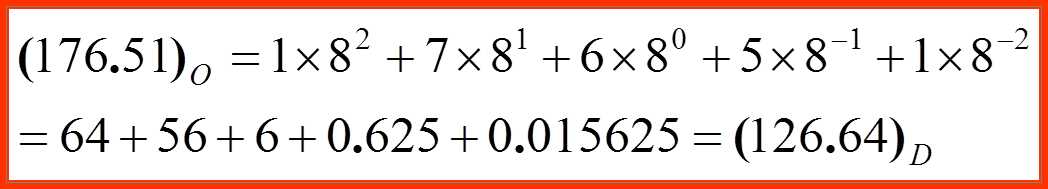
二、十进制数转换成二进制数：

即将十进制数转换成二进制数，原则是“整数除2，小数乘2

a. 十进制的整数转换：

将十进制的整数部分用基数2去除，保留余数，再用商除2，依次下去，直到商为0为止，其余数即为对应的二进制数的整数部分

b. 十进制的小数转换

将小数用基数2去乘，保留积的整数，再用积的小数继续乘2，依次下去，直到乘积是0为或达到要求的精度，其积的整数部分即为对应的二进制数的小数部分

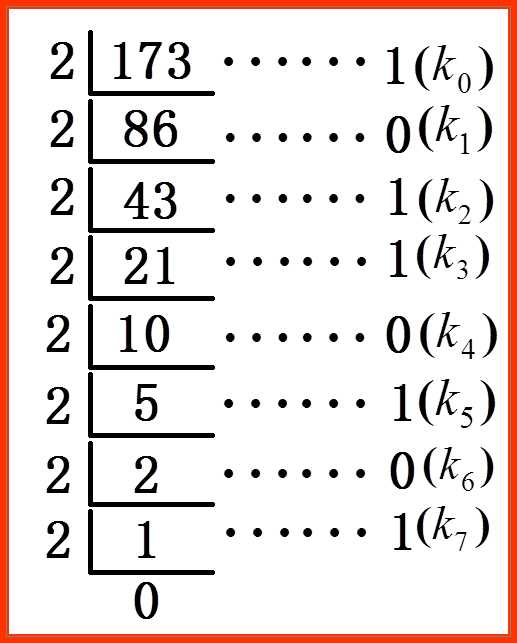
例  将（173.39)_D转化成二进制数,要求精度为1%

解：其过程如下

a. 整数部分 

即(173)_D=(10101101) _B

b. 小数部分

由于精度要求为1％，故应该令2^-m≤1% 取对数可得2^-m≤10^-2 ;2^m≥100;mlg₁₀²≥lg_{10¹⁰⁰;m≥6.6}

取m＝7 满足精度要求，过程如下

即(0.39)D=(0.0110001) B

故（173.39)D=(10101101.0110001)B

依此类推，对于十进制转换成其它进制，只要把基数2换成其它进制的基数即可。

三、 二进制转换成八进制和十六进制

方法：由于3位二进制数可以有8个状态，000~111，正好是8进制，而4位二进制数可以有16个状态，0000～1111，正好是16进制，故可以把二进制数进行分组。八进制三位分为一组，不够补零，十六进制四位分为一组。

注：若将八进制或十六进制转换成二进制，即按三位或四位转成二进制数展开即可。

提醒：若要将十进制转换成八进制或16进制，可先转换成二进制，再分组，转换成八进制或十六进制。

 二进制的算术运算

二进制算术运算的特点

当两个二进制数码表示两个数量的大小，并且这两个数进行数值运算，这种运算称为算术运算。其规则是“逢二进一”、“借一当二”。算术运算包括“加减乘除”，但减、乘、除最终都可以化为带符号的加法运算。

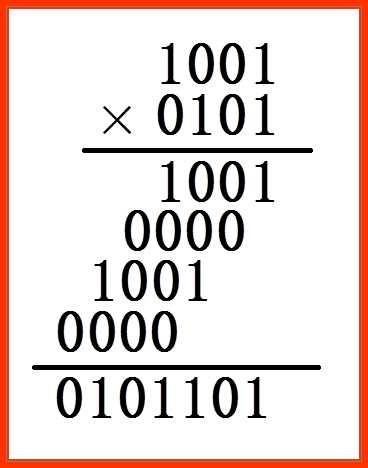
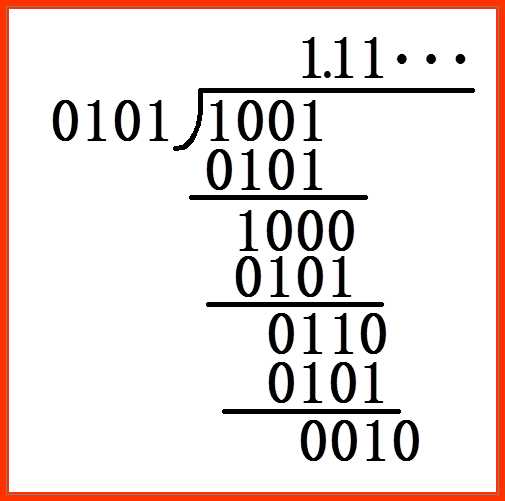
如两个数1001和0101的算术运算如下

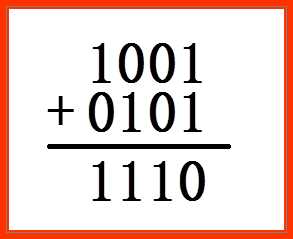
反码、补码和补码运算

一、原码：

在用二进制数码表示一个数值时，其正负是怎么区别的呢？二进制数的正负数值的表述是在二进制数码前加一位符号位，用“0”表示正数，用“1”表示负数，这种带符号位的二进制数码称为原码。

例如：＋17的原码为010001，－17的原码为110001

二、反码

反码是为了在求补码时不做减法运算。二进制的反码求法是：正数的反码与原码相同，负数的原码除了符号位外的数值部分按位取反，即“1”改为“0”，“0”改为“0”。

例如＋7和－7的原码和补码为：

＋7的原码为0  111，反码为0  111

－7的原码为1  111，反码为1  000

注：0的反码有两种表示，＋0的反码为0 000，－0的反码为1 111

三、补码：

当做二进制减法时，可利用补码将减法运算转换成加法运算。在将补码之前先介绍模（或模数）的概念

1.模（模数）的概念：

把一个事物的循环周期的长度，叫做这个事件的模或模数。

如一年365天，其模数为365；钟表是以12为一循环计数的，故模数为12。十进制计数就是10个数码0～9，的循环，故模为10。

以表为例来介绍补码运算的原理：对于图所示的钟表

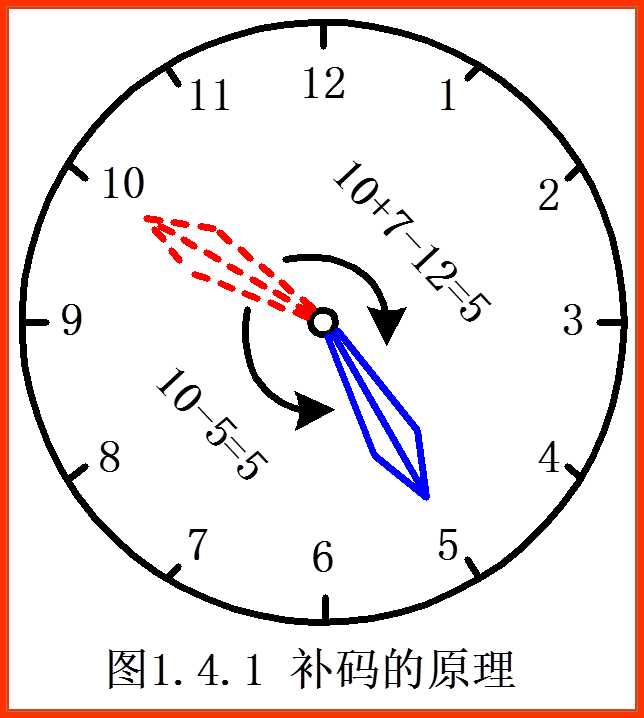
当在5点时发现表停在10点，若想拨回有两种方法：

a.逆时针拨5个格，即10－5＝5，这是做减法。

b.顺时针拨七个格，即10＋7＝17，由于模是12，故1相当于进位12，1溢出，故为7格，也是17－12＝5，这是做加法。

由此可见10＋7和10－5的效果是一样的，而5＋7＝12，将故7称为－5的补数，即补码，也可以说减法可以由补码的加法来代替。

2.补码的表示

正数的补码和原码相同，负数的补码是符号位为“1”，数值位按位取反加“1”，即“反码加1”。

例如：　　  原码　　   反码　　 补码

　　+7　　0 111　　0 111　　0 111

　　-7　　1 111　　1 000　　1 001

注意：

1.采用补码后，可以方便地将减法运算转换成加法运算，而乘法和除法通过移位和相加也可实现，这样可以使运算电路结构得到简化；

2.正数的补码既是它所表示的数的真值，负数的补码部分不是它所示的数的真值。

3.与原码和反码不同，“0”的补码只有一个，即（00000000）_B

4.已知原码，求补码和反码：正数的原码和补码、反码相同；负数的反码是符号位不变，数值位取反，而补码是符号位不变，数值位取反加“1”。

如：原码为10110100，其反码为11001011，补码为1100100。

5.已知补码，求原码：正数的补码和原码相同；负数的补码应该是数值位减“1”再取反，但对于二进制数来说，先减“1”取反和先取反再加“1”的结果是一样的。故由负数的补码求原码就是数值位取反加“1”。

如已知某数的补码为（11101110）_B，其原码为（10010010）_B

6.如果二进制的位数为n，则可表示的有符号位数的范围为（－2ⁿ～ 2^n－1－1），如n＝8，则可表示(－128～127)，故在做加法时，注意两个数的绝对值不要超出它所表示数的范围。

4位带符号位二进制代码的原码、反码和补码对照表

二进制编码

三个术语

数码：代表一个确切的数字，如二进制数，八进制数等。

代码：特定的二进制数码组，是不同信号的代号，不一定有数的意义。

编码：n 位二进制数可以组合成2n 个不同的信息，给每个信息规定一个具体码组，这种过程叫编码。 数字系统中常用的编码有两类，一类是二进制编码，另一类是  二-十进制编码。另外无论二进制编码还是二－十进制编码，都可分成有权码（每位数码代表的权值固定）和无权码。

十进制编码

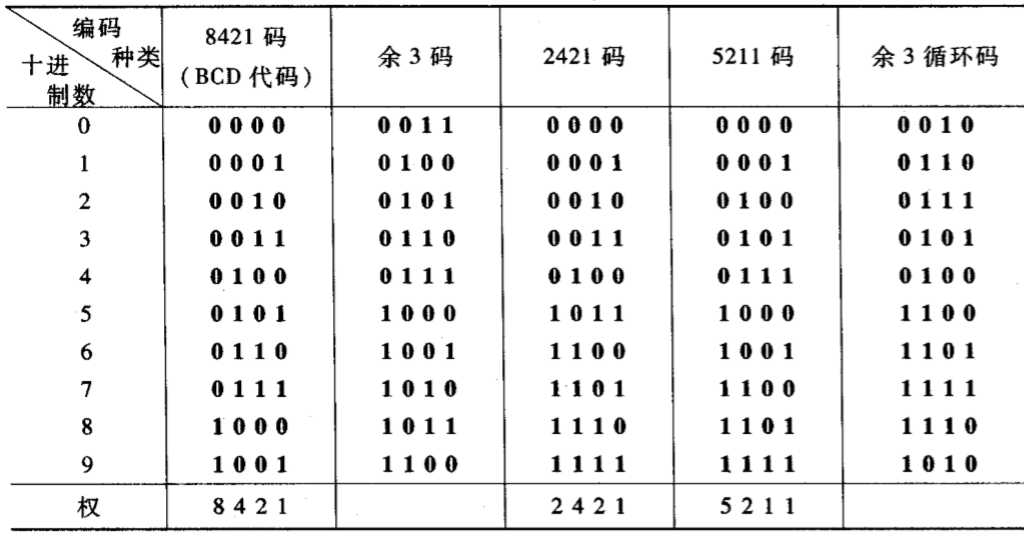
用4位二进制代码表示十进制的0～9个数码，即二－十进制的编码。 4位二进制代码可以有0000～1111十六个状态，则表示0～9十个状态可以有多种编码形式，其中常用的有8421码、余3码、2421码、5211码、余3循环码等，其中8421码、2421码、5211码为有权码，即每一位的1都代表固定的值。

几种编码形式

说明：

1. 8421码:又称BCD码，是最常用的十进制编码。其每位的权为8、4、2、1，如（0101）₂＝1×4＋1×1＝5

2. 余3码不是有权码，由于它按二进制展开后十进制数比所表示的对应的十进制数大3。如0101表示的是2，其展开十进制数为5，故称为余3码。采用余3码的好处是：利用余3码做加法时，如果所得之和为10，恰好对应二进制16，可以自动产生进位信号。如0110（3）＋1010（7）＝1111（10）；另外0和9、1和8、2和7…是互为反码，这对于求补很方便。

3. 2421码是有权码，其每位的权为2、4、2、1，如(1100)₂=1×2＋1×4＝6，与余3码相同0和9、1和8、2和7…是互为反码。另外当任何两个这样的编码值相加等于9时，结果的4个二进制码一定都是1111。

4. 5211码也是有权码，其每位的权为5、2、1、1，如(0111)2=1×2＋1×1＋1×1＝4，主要用在分频器上。

5. 余3循环码是无权码，它的特点是相邻的两个代码之间只有一位状态不同。这在译码时不会出错（竞争－冒险）

二进制编码：

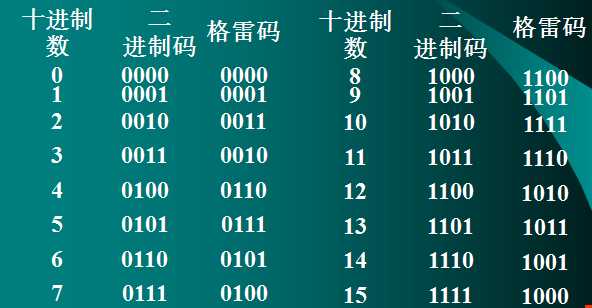
它包括自然码和循环码（格雷码）

自然码：有权码，每位代码都有固定权值，结构形式与二进制数完全相同，最大计数为2^n－1，n为二进制数的位数。

循环码：也叫格雷码，它是无权码，每位代码无固定权值，其组成是格雷码的最低位是0110循环；第二位是00111100循环；第三位是0000111111110000循环，以此类推可以得到多位数的格雷码。格雷码的特点是任何相邻的两个码组中，仅有一位代码不同，抗干扰能力强，主要用在计数器中。

第一章：数制和码制

标签：

原文地址：http://www.cnblogs.com/tmluan/p/4841456.html