欧拉定理

标签：

我们令 Ψ(x) 定义为欧拉函数。

• 欧拉定理描述 ： 

　　　　若 (a , p) = 1 , 那么 a^Ψ(p) Ξ 1 (mod p) .

• 证明：

　　　　先预热一下：

　　　　Ⅰ.我们令 x₁ , x₂ , x₃ , ……, x_s 为 模p 的简化剩余系 (若果对任意的1 ≤ j ≤ s , (x_j , p) = 1 并且对于任意的 a ∈ Z ,若 (a , p) = 1 , 那么有且仅有一个 x_j 是 a 对 模p 的剩余（及x_i两两不相同) _.)其中 s = ψ(p) .

　　　　Ⅱ. 若 {x₁,x₂,x₃,……，x_s} 为 mod p 的简化剩余系 ， 那么若 (k , p) = 1 , {k·x₁,k·x₂,k·x₃,……，k·x_s}也为 mod p 的简化剩余系 ， 证明：

　　　　　　　　若{k·x₁,k·x₂,k·x₃,……，k·x_s}不是 mod p的 简化剩余系 ， 

　　　　　　　　那么至少存在一组 k·x_i Ξ k·x_j (mod p) , i != j :

　　　　　　　　　　　　∴ k · (x_i - x_j) Ξ 0 (mod p) 

　　　　　　　　　　　　又∵ (k , p) = 1 , ∴(x_i - x_j) Ξ 0 (mod p) ;

　　　　　　　　　　　　这与 x_i ，x_j∈ {mod p 的简化剩余系} 相矛盾 ， 所以假设不成立 ， 及若 (k , p) = 1 , {k·x₁,k·x₂,k·x₃,……，k·x_s}也为 mod p 的简化剩余系成立。

　　接下来开始真正的证明 ：

　　　　　　我们令 {a₁ , a₂ , a₃ , …… ， a_n}为 mod p 的简化剩余系 ，因为欧拉定理中 (a , p) = 1 , 所以 {a·a₁ , a·a₂ , a·a₃ , …… ，a·a_n} 也为 mod p 的简化剩余系 。

　　　　　　∴ a₁ · a₂ · a₃ · …… · a_n Ξ a·a₁ · a·a₂ · a·a₃ · …… · a·a_n Ξ a^Ψ(p) · a₁ · a₂ · a₃ · …… · a_n (mod p) ;

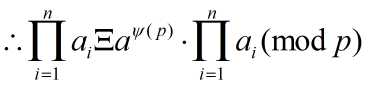
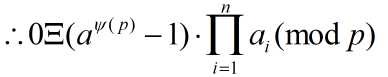
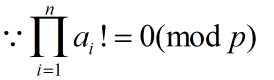
　　　　　　∴ a^ψ(p) - 1 Ξ 0 (mod p) , ∴ a^ψ(p) Ξ 1 (mod p) 得证 。

• 欧拉定理的简单应用：

　　　　　　求 a^x mod p  , 其中 （a ， p）= 1 。

　　　　　　x = s · ψ(p) + q , q < ψ(p)

　　　　　　∴ a^x Ξ a^{s · ψ(p) + q}  Ξ (a^ψ(p))^s · a^q Ξ a^q Ξ a^{x mod p} (mod p)

欧拉定理

标签：

原文地址：http://www.cnblogs.com/get-an-AC-everyday/p/4843233.html