标签:
上一篇中用一个直观的例子描述了贝叶斯学习的过程,现在我们看看在数学模型下具体的描述。
1. 贝塔-二项分布
首先又是万年不变的丢硬币的例子:小明和老婆抛硬币决定谁洗碗,小明总是担心老婆在硬币上动了手脚,他决定利用以往的数据估算硬币正面朝上的概率。
假设硬币的朝向服从伯努利分布,在一系列的投掷过程中,有N1次正面朝上,N0背面朝上,则能够很轻易得出此次抛投的概率:
![]()
当然这是对任意一次的抛投过程来说的,如果我们知道某一次投掷过程的具体的结果,想求出现这次结果的概率,前面就需要乘以一个组合的系数,即
![]()
问题的关键在于,先验概率应该如何确定。理论上来说任何一个在[0,1]上支撑的分布函数都能够符合条件,但是小明希望能够使结果尽可能地简化。最理想的情况,就是先验分布和似然分布拥有相同的形式,即:
![]()
那么后验分布可以很轻易地得到:只需要把指数相加即可
![]()
计算果然很简单,想到这里,小明幸福地留下眼泪。
幸运的是,有一个很常见的分布正好满足这种形式,它就是 Beta 分布。
![]()
具体来说,如果我们对先验的分布一无所知的话,令a=b=1即可。如果想附加信息进入的话,则可以通过计算得出具体的参数值。在MLPP中给出的例子是,如果我们认为先验分布θ
具有0.7的方差和0.2的标准差,则令a=2.975,b=1.275。
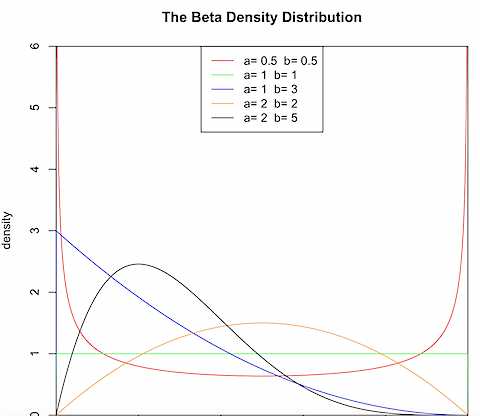
下图是我在R语言中展示的几个Beta函数的密度函数。
。
一个比较直观的理解方式是,先验分布的加入相当于一个伪计数(pseudo counts)。先验信息的加入相当于预先按照先验分布的设定投掷了一定数量的硬币,最后的结果也就是实际投掷结果和先验分布的综合。
那么问题来了,小明在之前20次的投掷硬币中,一共投出了3次正面。理论上说硬币朝上的概率约为15%。但此时出于对老婆良心的肯定,我们设定先验分布为Beta(4,4)。那么硬币朝上的概率会被提高到20%以上(不过还是很低,小明感到一阵心酸)
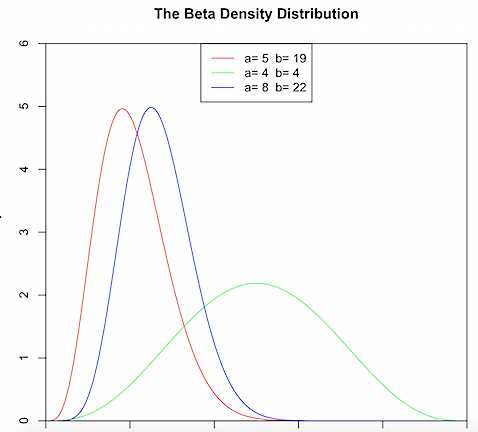
那么加入先验分布的意义是什么呢?相信大家都知道“黑天鹅事件“这个俗语。比如说连续投掷5次硬币每次都为正面的概率非常小,但是一旦发生,那么硬币朝上的似然概率就为1,这样似乎会违背我们的常识。但是如果我们加入一个均值为0.5的先验分布,就能够将正面朝上的概率往0.5“拉”一点,这样就能够有效地应对“黑天鹅事件”的发生。
标签:
原文地址:http://www.cnblogs.com/cklwanfifa/p/4845060.html