标签:
同一坐标系下的点旋转变换(如图1所示)和不同坐标系下的点变换(如图2所示),一直困扰着我,它们是两个不同的概念,但形式上有很相似,以二维空间为例做了下推导,加深理解。
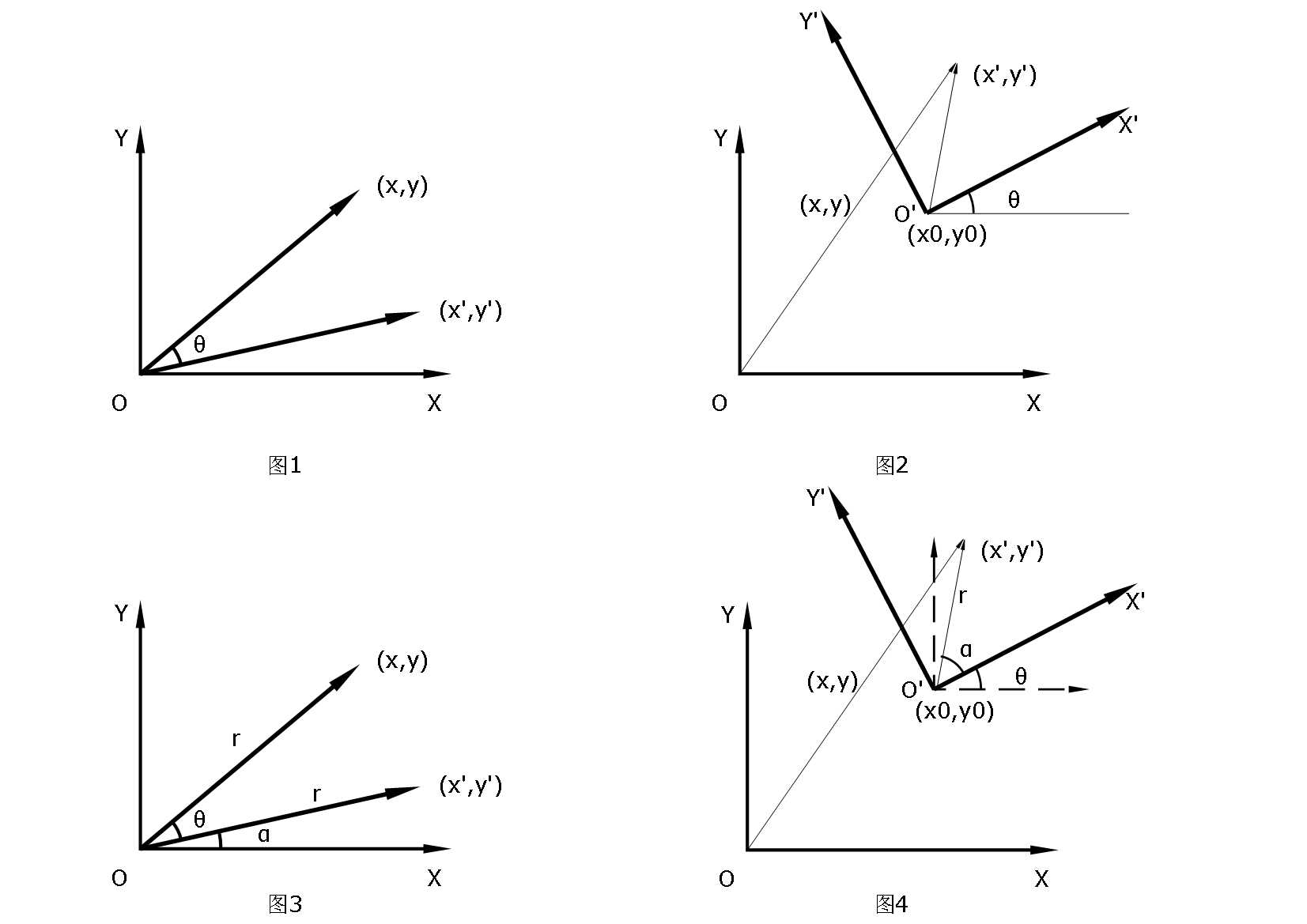
同一坐标系下的点旋转变换,比较好理解,是在相同的坐标系下做的旋转变换。如图3所示,已知逆时针的旋转角度为θ,我们引入中间变量向量的长度r和水平夹角α,显而易见地,推导公式如下:
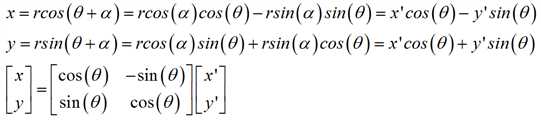
齐次坐标系的表达为:
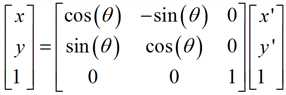
不同坐标系下的点变换,这是透视变换中常用到的,它的作用是将一个点从一个坐标系统映射到另一个坐标系统下,这在将世界坐标系统映射到像极坐标系统中是很有用的。如图4所示,已知坐标系O‘X‘Y‘相对于OXY坐标系逆时针的旋转角度为θ,O‘X‘Y‘的坐标原点O‘相对于OXY的坐标为(x0,y0),我们引入中间变量向量的长度r和水平夹角α。变换的思路是,先对O‘X‘Y‘坐标系旋转θ,然后在平移(x0,y0)。推导过程如下:
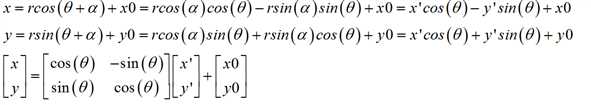
齐次坐标系的表达为:
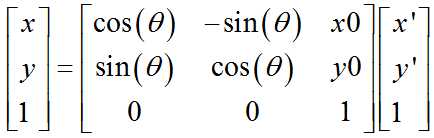
注意齐次坐标的作用是把旋转缩放和平移结合起来,在传统的欧几里得空间中是做不到的,需要在投影空间中的齐次坐标系统下完成。
同理可以扩展到三维空间。OXYZ坐标系统可以看作是相机坐标系统,O‘X‘Y‘Z‘可以看做世界坐标系统,
参考资料:
[1].矩阵的坐标变换(转)(里面介绍了矩阵的旋转缩放,还有推导过程,强烈推荐★★★★★)
标签:
原文地址:http://www.cnblogs.com/cv-pr/p/4850465.html