线段树(segment tree)

时间：2015-10-01 11:29:43 阅读：178 评论：0 收藏：0 [点我收藏+]

标签：

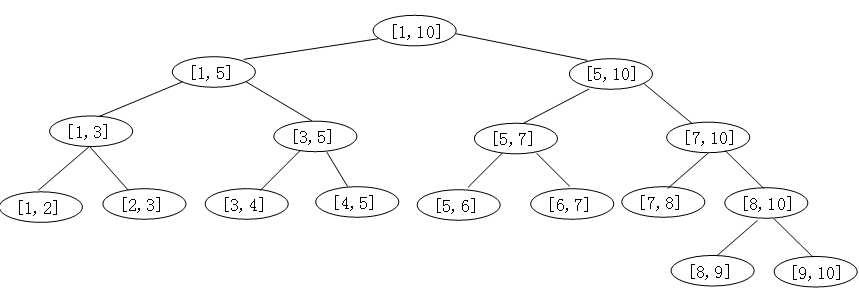
线段树是一棵二叉树，记为T(a, b)，参数a,b表示区间[a,b]，其中b-a称为区间的长度，记为L。

技术分享

数据结构：

struct Node
{
    int   left,right;  //区间左右值
    Node   *leftchild;
    Node   *rightchild;    
};

线段树的建立：

Node   *build(int   l ,  int r ) //建立二叉树
{
    Node   *root = new Node;
    root->left = l;
    root->right = r;     //设置结点区间
    root->leftchild = NULL;
    root->rightchild = NULL;

    if ( l +1< r ) //L>1的情况，即不是叶子结点
    {
       int  mid = (r+l) >>1;
       root->leftchild = build ( l , mid ) ;
       root->rightchild = build ( mid  , r) ; 
    } 
    return    root; 
}

插入一条线段[c,d]：

增加一个cover的域来计算一条线段被覆盖的次数，在建立二叉树的时候应顺便把cover置0。

void  Insert(int  c, int d , Node  *root )
{
       if(c<= root->left&&d>= root->right) 
           root-> cover++;
       else 
       {
           //比较下界与左子树的上界
           if(c < (root->left+ root->right)/2 ) Insert (c,d, root->leftchild  ); 
           //比较上界与右子树的下界
           if(d > (root->left+ root->right)/2 ) Insert (c,d, root->rightchild  );
//注意，如果一个区间横跨左右儿子，那么不用担心，必定会匹配左儿子、右儿子中各一个节点
       }
}

删除一条线段[c,d]:

void  Delete (int c , int  d , Node  *root )
{
       if(c<= root->left&&d>= root->right) 
           root-> cover= root-> cover-1;
       else 
       {
          if(c < (root->left+ root->right)/2 ) Delete ( c,d, root->leftchild  );
          if(d > (root->left+ root->right)/2 ) Delete ( c,d, root->rightchild );
       }
}

QUESTION：

Given a huge N*N matrix, we need to query the GCD(greatest common divisor最大公约数) of numbers in any given submatrix range（x1,y1,x2,y2）. Design a way to preprocess the matrix to accelerate the query speed. extra space should be less than O(N^2) and the preprocess time complexity should be as litte as possible.

SOLUTION：

For each row A[i] in the matrix A, we build a segment tree.The tree allows us to query GCD(A[i][a..b]) 第i行第a到b列（不包括b)的最大公约数in O(log n) time . The memory complexity of each segment tree is O(n), which gives us O(n^2) total memory complexity.

时间复杂度，O(n2)建立线段树， O(r * log(c)) 查找，其中r and c are the number of rows and columns in the query.

GCD的实现：被除数与余数对于除数同余，所以被除数与除数的GCD就是余数与除数的GCD，所以用递归或循环求解。

int a = 45, b = 35,tmp;
while(b!=0){
a = a%b;
tmp = a;
a = b;
b = tmp;
}
cout << a << endl;

线段树(segment tree)

标签：

原文地址：http://www.cnblogs.com/qionglouyuyu/p/4850774.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行