标签:
RB树(红黑树)并不追求“完全平衡”——它只要求部分地达到平衡要求,降低了对旋转的要求,从而提高了性能。由于它的设计,任何不平衡都会在三次旋转之内解决。典型的用途是实现关联数组(如C++中的map和set)
只有满足一下性质的树,我们才称之为红黑树:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
RB树插入节点的步骤:我们用日本武士的阶层来做比喻。新插入的节点为红色。插入操作时,好像一个新的武士出仕,没有背景,没有功勋。但他有能力,有抱负,就像丰臣秀吉那样。
按照二叉查找树的规则插入新节点后,如果新增节点的父节点为黑,则直接插入(跟了个黑色类型的主公,虽然终究会不甘心居人之下,但却没条件“下克上”)。否则因为红节点的儿子节点必须是黑节点,所以要做调整,分为4种情况(在此作一些符号约定,新增节点为X,其父节点为P,祖父节点为G,伯父节点为S,曾祖父节点为GG):
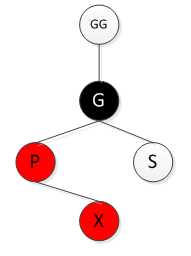
1) S为黑,且X为外侧插入。P,G做一次单旋转,并更改P,G的颜色。(类似于AVL树外侧插入单旋转)
要是大主公其他家臣是碌碌之辈,主从两个造反成功!成功后,原来大主公成了主公的家臣,忍辱负重,卧薪尝胆,等待重新崛起的时机;而主公这一家,上位后,家风就堕落了。
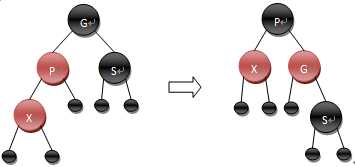
2) S为黑,且X为内侧插入。X,P做一次单旋转,并更改X和P的颜色;再对X,G做一次单旋转。(类似于AVL树内侧插入双旋转)
野心更大的做法是,跟大主公报告主公谋反。反正主公忠心有限,把柄很多。于是新武士举报有功,主公反倒成了自己的家臣。昏庸的大主公很快就要付出代价,自己成了新武士的下一个目标。
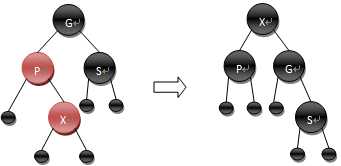
3) S为红,且X为外侧插入。 P,G做一次单旋转,并更改X的颜色。此时如果GG为黑,一切搞定;否则,还得继续往上做,直到不再有父子节点连续为红的情况。(类似于AVL树外侧插入单旋转)
其他家臣一样有能力,但主公更强大成功上位。因为有着强大的主公,新武士碌碌无为自甘堕落了。
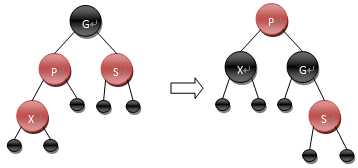
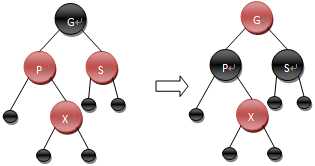
4)S为红,且X为内侧插入。直接更改P,S,G的颜色。此时如果GG为黑,一切搞定;否则,还得继续往上做,直到不再有父子节点连续为红的情况。
其他家臣一样有能力,大主公能力平庸,控制不住,最终酿成大乱,经过一番血雨腥风,大主公家出现了一位雄才伟略的家主,平定了内乱,原来两家家臣的强势家主全部被消灭,家主换成了忠心可靠的人。而大主公家的新家主,野心开始膨涨了。
为了避免上述情况3、4中GG也为红的情况发生,我们设计一个“自顶向下”的红黑树。假设新增节点为A,那么就延着从根节点到A的路径,只要看到某个节点X的两个子节点皆为红色,就把这两个子节点改为黑色,同时把X改为红色。但是如果此时X的父节点也是红色(注意此时X的伯父节点已经不可能是红色),就像上述情况1那样作一次单旋转改变颜色,或像情况2那样做一些双旋转再改变颜色。
标签:
原文地址:http://www.cnblogs.com/qionglouyuyu/p/4850733.html