标签:
主要内容:
1、距离度量
2、皮尔逊关系系数
3、cosine相似度
4、方法的选择
距离度量是最简单的衡量相似度的方法,公式如下:
当r=1时,为曼哈顿距离(manhattan distance);
当r=2时,为欧几里得距离(Euclidean distance);
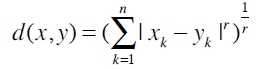
优点:简单
缺点:当数据某些属性或特征缺失时,该度量结果不准确
代码:
def minskowski(rating1,rating2,r): distance=0 commonRatings=Flase for key in rating1: for key in rating2: distance+=pow(abs(rating1[key]-rating2[key]),r) commonRatings=True if commonRatings: return pow(distance,1/r) else: return 0 #indicates no ratings in common
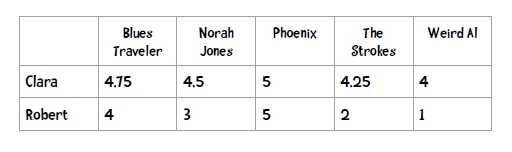
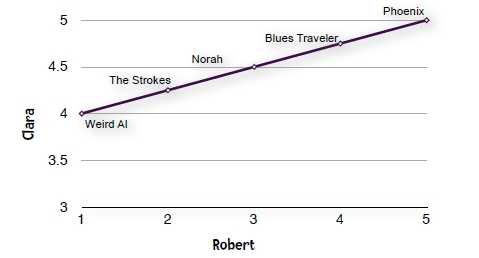
有时候,每个人的判断标准不一样,例如在给物品打分(1-5)时,有的人的打分范围为4-5,而有的人为1-5,而他们其实的评价结果是一样的。
但如果通过上述的距离度量的话,那么这两个人的相似度则会相差甚远,因此需要一种类似归一化的方法来解决。
公式如下:
r范围为-1~1
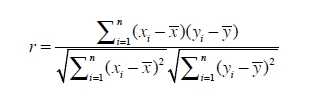
在实际代码实现中,也可以写成下面的形式,这样子就只需要遍历一遍数据即可。
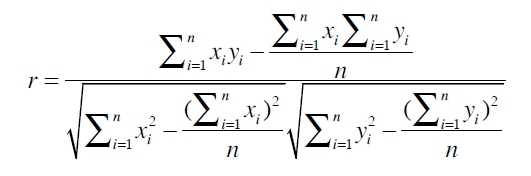
代码:
def pearson(rating1, rating2): sum_xy = 0 sum_x = 0 sum_y = 0 sum_x2 = 0 sum_y2 = 0 n = 0 for key in rating1: if key in rating2: n += 1 x = rating1[key] y = rating2[key] sum_xy += x * y sum_x += x sum_y += y sum_x2 += pow(x, 2) sum_y2 += pow(y, 2) # now compute denominator denominator = sqrt(sum_x2 - pow(sum_x, 2) / n) * sqrt(sum_y2 - pow(sum_y, 2) / n) if denominator == 0: return 0 else: return (sum_xy - (sum_x * sum_y) / n) / denominator
在距离度量中提到,特征空间往往都是稀疏的,如果通过距离去度量相似性的话,会出现不准确的结果。
因此,cosine相似度计算可以解决这个问题,因为它会忽略0值的计算,公式如下:
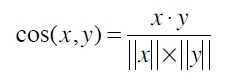
代码:
def cosine(rating1, rating2): sum_xy = 0 sum_x2 = 0; sum_y2 = 0 for key in rating1: sum_x += rating1[key] * rating1[key] for key in rating2: sum_y += rating2[key] * rating2[key] for key in rating1: for key in rating2: sum_xy += rating1[key] * rating2[key] denominator = sqrt(sum_x2) * sqrt(sum_y2) if denominator == 0: return 0 else: return sum_xy / denominator
如果数据是密集dense,那么可以用距离度量;
如果数据是稀疏的sparse,那么可以用cosine度量;
如果数据尺度不一致,那么可以用pearson度量;
标签:
原文地址:http://www.cnblogs.com/AndyJee/p/4852004.html