标签:
本文实现基于SVD奇异矩阵分解的PCA主成分分析,使用该算法来完成对人脸图像的识别,主要讲解SVD实现PCA的原理,如何利用SVD实现图像特征的降维,以及SVD在文本聚类方面的使用,例如弱化同义词、多义词的影响,解决传统文本向量空间无法解决的问题。
本次实验需求分析很简单,实现人脸图像识别,简单地模仿谷歌、百度的识图搜索功能。
特征用来区别一个事物属于哪种类别,例如“是否有翅膀”可以拿来区别麻雀和哈士奇。如何判别两幅图是否是同一个人,我们可以选取图像的像素矩阵构成特征向量,例如一副180 * 200的jpg图像,根据其像素矩阵可以构成一个特征向量vector[180 * 200],有了特征向量我们就可以使用欧氏距离、余弦相似度等计算两幅图的相似度,从而得出是否属于同一个人。
直接使用像素矩阵构成特征向量,当图像很大时计算难免耗时Time Limited,我们将像素称为原始特征。如何将原始特征向量降维,同时又保存它的主要特性,我们可以联想到PCA主成分分析。在PCA主成分分析中,有一种奇异矩阵分解SVD算法,原矩阵可以分解为 M = U x S x V‘,然后选取前 k 个重要的特征组成新的特征向量完成降维。例如上例,k=20时,可以组成新的特征向量vec‘[180 * 20 + 200 * 20],计算量大大减少又不影响比较结果。接下来,我们就来看一下SVD是个是么东西。
SVD入门基础三步曲:
(1)机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用
(2)【译】从几何角度看SVD
(3)奇异值分解和图像压缩
看完上面3篇也就大概知道SVD的原理是什么了,矩阵U由左奇异特征向量组成(描述y轴方向的变化趋势),矩阵S代表对于左(右)特征向量的重要性,矩阵V‘ 由右奇异特征向量组成(描述x轴方向的变化趋势)。
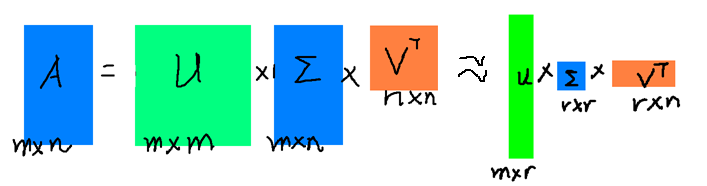
由SVD原理可知,我们可以选取前r 个左奇异特征向量、前r 个右奇异特征向量,组成一个新的特征向量vec[ m * k + n * k],从而完成降维,减少计算量而又保佑原有人脸图像特性。
模型特征向量选取完成后,我们就可以拿来比较两幅人脸图像的相似性了。在计算图像相似性时,本文采用余弦相似度算法进行比较,算法代码实现如下:
Pca.java
package key;
import java.awt.image.BufferedImage;
import java.io.File;
import java.io.IOException;
import javax.imageio.ImageIO;
import Jama.*;
public class Pca {
public double Cosine(double[] v1, double[] v2) {
double ans = 0;
int n = v1.length;
double a = 0;
for (int i = 0; i < n; i++) {
a += v1[i] * v2[i];
}
double b = 0;
for (int i = 0; i < n; i++) {
b += v1[i] * v1[i];
}
b = Math.sqrt(b);
double c = 0;
for (int i = 0; i < n; i++) {
c += v2[i] * v2[i];
}
c = Math.sqrt(c);
ans = a / b / c;
return ans;
}
public double[] PcaVector(double[][] pixels, int k) {
Matrix ps = Matrix.constructWithCopy(pixels);
if (ps.getRowDimension() < ps.getColumnDimension()) {
ps = ps.transpose();
}
SingularValueDecomposition svd = ps.svd();
Matrix u = svd.getU();
Matrix s = svd.getS();
Matrix vt = svd.getV().transpose();
double[] vec = new double[u.getRowDimension() * k
+ vt.getColumnDimension() * k];
int cur = 0;
for (int i = 0; i < k; i++) {
for (int j = 0; j < u.getRowDimension(); j++) {
vec[cur + i * u.getRowDimension() + j] = u.get(j, i);
}
}
cur += u.getRowDimension() * k;
for (int i = 0; i < k; i++) {
for (int j = 0; j < vt.getColumnDimension(); j++) {
vec[cur + i * vt.getColumnDimension() + j] = vt.get(i, j);
}
}
return vec;
}
public double[][] Pixels(File file) throws IOException {
BufferedImage bi = ImageIO.read(file);
int h = bi.getHeight();
int w = bi.getWidth();
double arr[][] = new double[w][h];
for (int i = 0; i < w; i++) {
for (int j = 0; j < h; j++) {
arr[i][j] = bi.getRGB(i, j);
}
}
return arr;
}
}
Keyven.java
package key;
import java.io.File;
import java.io.IOException;
public class Keyven {
public static void main(String[] args) throws IOException {
Pca pk = new Pca();
int k = 20;
File key = new File("data/key.jpg");
double[] vec_key = pk.PcaVector(pk.Pixels(key), k);
File folder = new File("data/faces");
if (folder.isDirectory()) {
for (File f : folder.listFiles()) {
double[] vec_f = pk.PcaVector(pk.Pixels(f), k);
System.out.println(f.getName() + ":\t"
+ pk.Cosine(vec_key, vec_f));
}
}
}
}
原图像集和候选搜索图像如下:


我们来看一下实验效果:


对比还是蛮不错的^_^!
上面讲到左奇异特征向量代表y轴的变化趋势,右奇异向量代表x轴的变化趋势,想象用在自然语言处理文本聚类中,有一个文档-词项共现矩阵,使用SVD作主成分分析,有可能使得原共现矩阵里正交的向量变得不正交,从而弱化了同义词、多义词的影响,而不是简简单单地依靠一个词是否在一篇文档中出现过来造特征……
标签:
原文地址:http://my.oschina.net/keyven/blog/513396