标签：
问：给你k种颜色，你必须用上所有颜色去涂满n个相邻的格子，并且要求相邻格子的颜色不同，求方案数。
我们设必须用 i 种颜色两两不相邻的涂格子的方案数为 b(i) ;
很明显: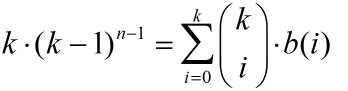 
,我们令 a(k)=k·(k-1)n-1 , 然后有
.
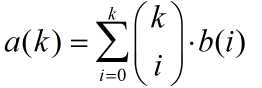如果你知道二项式反演的话，那么这个问题就已经解决了，因为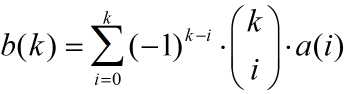
.
是不是觉得二项式反演很厉害，下面我将给出它的证明。
然后让我们对
进行分析：
我们预热一下：
有A,B,C,D,E,F,G 7个人，我们要先从中选出4个候选人,再从中选出3个作为master。
那么我们可以很容易写出其方案数：
但是我们用另一种邪恶的思路思考这个问题：
我们可以先内部选出3个master，在从剩下的4个人选出一个来：
。
所以我们很容易的得到了这个等式：
所以有
然后你会发现剩下的部分就是 （1 - 1）n-j的项张开而已，所以：
，所以原式 = b(n) .
所以：成立。
#include<bits/stdc++.h>
using namespace std;
const int M = 1e6 + 10 ;
int n , m , k ;
const int mod = 1e9 + 7 ;
int key ;
int f[M] , inv[M] , finv[M] ;
void table () {
inv[1] = 1 ;
for (int i = 2 ; i < M ; i ++) inv[i] = (mod - mod/i) * 1ll * inv[mod%i] % mod ;
f[0] = finv[0] = 1 ;
for (int i = 1 ; i < M ; i ++) {
f[i] = 1ll*f[i-1] * i % mod ;
finv[i] = 1ll*finv[i-1] * inv[i] % mod ;
}
}
int qkpow (int a , int b) {
int ret = 1 ;
while (b) {
if (b & 1) ret = 1ll*ret*a % mod ;
b >>= 1 ;
a = 1ll*a*a%mod ;
}
return ret ;
}
int comb (int n , int m) {
if (m < 0 || n < m) return 0 ;
return 1ll * f[n] * finv[m] % mod * finv[n-m] % mod ;
}
int solve (int x) {
//cout << qkpow (-1 , k-x) << " " << comb (k,x) << " " << x << " " << qkpow (x-1 , n-1) << endl ;
return 1ll*qkpow(-1 , k-x) * comb (k , x) * x % mod * qkpow (x-1 , n-1) % mod ;
}
int main () {
int T ;
table () ;
scanf ("%d" , &T ) ;
for (int cas = 1 ; cas <= T ; cas ++) {
scanf ("%d%d%d" , &n , &m , &k) ;
printf ("Case #%d: " , cas ) ;
key = 0 ;
for (int i = 0 ; i <= k ; i ++) {
//puts ("heheh") ;
key = ((1ll*key + 1ll*solve (i) ) % mod + mod ) % mod ;
}
//puts ("======") ;
int ans = 1 ;
for (int i = 1 ; i <= k ; i ++) {
ans = 1ll*ans*(m-k+i)%mod ;
}
printf ("%d\n" , key*1ll*ans%mod*finv[k]%mod ) ;
}
return 0 ;
}
标签：
原文地址：http://www.cnblogs.com/get-an-AC-everyday/p/4855108.html
