假设要在n个城市之间建立通信联络网,则连通n个城市只需要n-1条线路。
这时, 如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置—条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n- 1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?
标签:
先来前排卖个瓜子,推荐个oj:一个神奇的oj
http://oj.fjaxyz.com:3389/problem.php?id=69
假设要在n个城市之间建立通信联络网,则连通n个城市只需要n-1条线路。
这时, 如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置—条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n- 1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?
这题是裸的最小生成树,何为最小生成树?就是一张图,n个点,n-1条边,且边上的权值加起来还要最小
这题的样例图如下
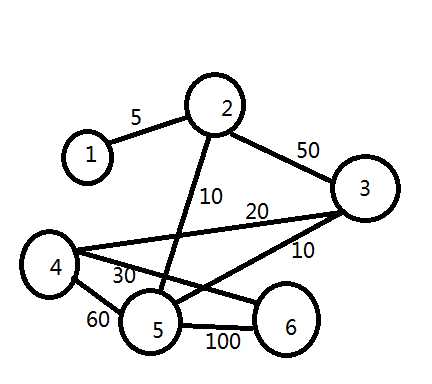
(画图技术不要吐槽)
这图的最小生成树就是
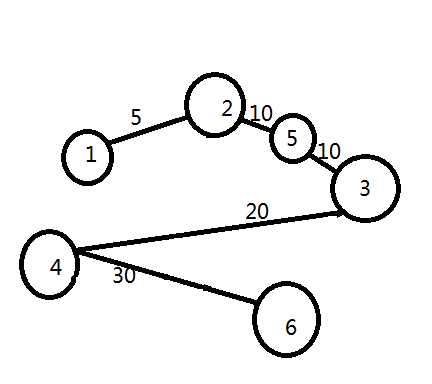
边上的权值相加就是75,就是最小生成树了
那么怎么知道是这样一棵树呢
最小生成树有两个做法
1.prim
2.克鲁斯卡(英语不行)
我的做法是克鲁斯卡的
克鲁斯卡的做法就是:
首先是排序边:
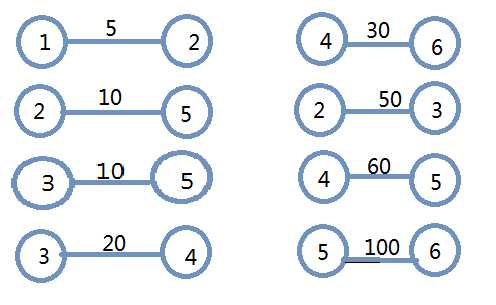
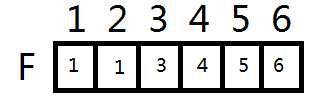
然后将并查集所需要的f数组初始化
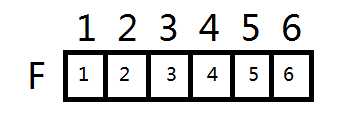
这里需要自行去查找并查集的写法
选取最小的边,也就是第一条
第一条边所连接的两个点是1,2
用并查集查找1和2的祖先
u=find(1),v=find(2)
发现u不等于v,我们就把他们并在一起即f[v]=u,这样下次查找祖先就可以找到同一个了
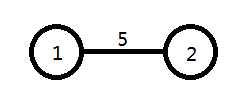
然后仿照刚刚的做法就可以把2和5也连接起来
但这里要记得是把f[5]赋值为2的祖先,即1
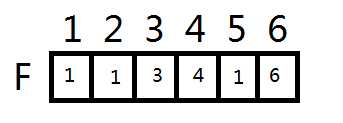
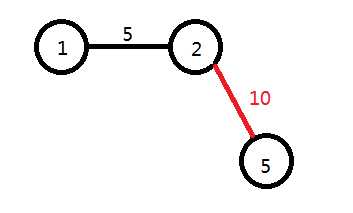
3和5的这一条也不多说的,直接上图
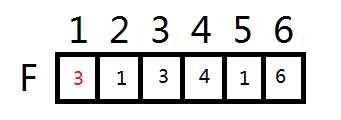
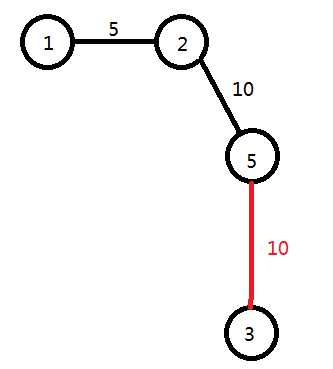
3和4,4和6的这两条也来了(唉,,图好多,,这是我画得最好的图了)
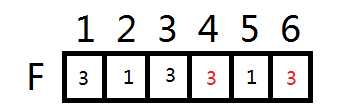
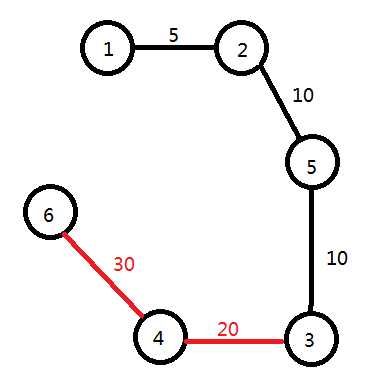
至此,一棵完美的最小生成树就完成了
但
如果程序试图往下继续搜索会怎样
比如到了2和3这一条
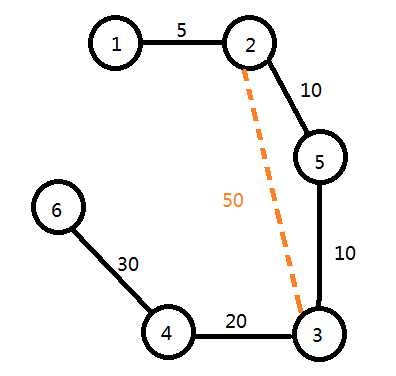
此时按照刚刚的步骤,它会先找2的祖先u=3,再找3的祖先v=3
这时我们发现两点已经连通,没必要再连一次了,所以就不会连了
也就是说判断是否连通只要判断u是否等于v
另外咱们选的边是从最小开始的选取,所以生成的树自然也就是最小的
用一句话概括:易证其正确性
所以我就不证了,剩下的内容自己脑补吧
如果前面都看懂了,那么恭喜你学会了最小生成树,等你代码写多了,你就会发现
这个算法其实并没有什么卵用,,,感觉很少用到的样子
要想考试拿高分,还得学爆搜啊:)

1 #include <cstdio> 2 #include <iostream> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 int f[300]; 7 struct graph 8 { 9 int from,to,dis; 10 }a[45000]; 11 bool cmp(graph x,graph y) 12 { 13 return x.dis<y.dis; 14 } 15 int find(int x) 16 { 17 return f[x]==x?x:f[x]=find(f[x]); 18 } 19 int main() 20 { 21 int n,b,k=1,i,j,x,y,ans=0; 22 scanf("%d",&n); 23 for(i=1;i<=n;i++) 24 f[i]=i; 25 for(i=1;i<=n;i++) 26 { 27 for(j=1;j<=n;j++) 28 { 29 scanf("%d",&b); 30 if(j<=i || b==-1) 31 continue; 32 a[k].from=i; 33 a[k].to=j; 34 a[k++].dis=b; 35 } 36 } 37 sort(a+1,a+k,cmp); 38 for(i=1;i<k;i++) 39 { 40 x=find(a[i].from); 41 y=find(a[i].to); 42 if(x!=y) 43 { 44 ans+=a[i].dis; 45 f[y]=x; 46 } 47 } 48 printf("%d\n",ans); 49 return 0; 50 }
标签:
原文地址:http://www.cnblogs.com/helloworld-c/p/4854215.html