ACM学习历程—HDU5476 Explore Track of Point（平面几何）（2015上海网赛09题）

标签：

Problem Description

In Geometry, the problem of track is very interesting. Because in some cases, the track of point may be beautiful curve. For example, in polar Coordinate system,ρ=cos3θ is like rose, ρ=1−sinθ is a Cardioid, and so on. Today, there is a simple problem about it which you need to solve.

Give you a triangle ΔABC and AB = AC. M is the midpoint of BC. Point P is in ΔABC and makes min{∠MPB+∠APC,∠MPC+∠APB} maximum. The track of P is Γ. Would you mind calculating the length of Γ?

Given the coordinate of A, B, C, please output the length of Γ.

Input

There are T (1≤T≤104) test cases. For each case, one line includes six integers the coordinate of A, B, C in order. It is guaranteed that AB = AC and three points are not collinear. All coordinates do not exceed 104 by absolute value.

Output

For each case, first please output "Case #k: ", k is the number of test case. See sample output for more detail. Then, please output the length of Γ with exactly 4 digits after the decimal point.

Sample Input

1

0 1 -1 0 1 0

Sample Output

Case #1: 3.2214

题目稍微转换一下就变成求∠MPB+∠APC=∠MPC+∠APB=180的点p的轨迹了。

这最后结论是一道平面几何题，高中数竞虽然搞过平面几何，不过基本全部忘光了，定理也只记得一个梅涅劳斯定理了。。。虽然当时就很弱。。

高中数竞时小烈平几就很强@hqwhqwhq，果然赛后题解交代了轨迹寻找的过程。。

http://blog.csdn.net/u014610830/article/details/48753415

虽然找的过程没怎么看懂，不过证明过程基本看懂了。

如果能猜出轨迹的话题目也就解决了，剩下就是怎么证明这个轨迹满足条件了。

首先三角形的高AM是满足条件的，基本是没问题的。

其次B和C点在极限情况下发现也是满足条件的，由于对称性，基本上剩余轨迹就是过B和C的一种图形。。。

运气好的话猜到它是个圆就能解决。。。

盗一张图：

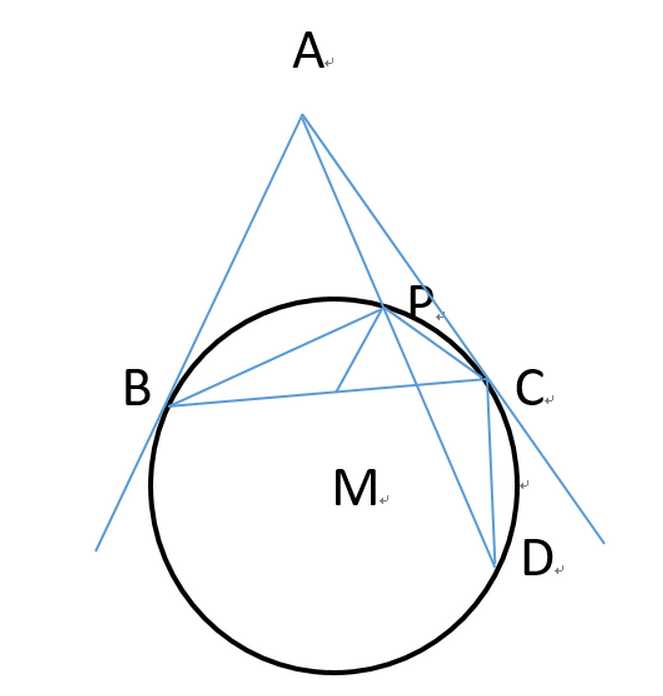
结论是剩余的图是AB过B的垂线与AC过C的垂线交于点M，以M为圆心，BM为半径的圆弧。

接下来证明：

对于圆弧上某一点P，AP延长交圆于点D，

目测的话，∠BPM = ∠CPD。结论就是这个，接下来就是证明这个。

由于B、P、C、D四点共圆，根据托勒密定理：

CP*BD+BP*CD = BC*DP

由根据割线定理：

AB*AB = AP*AD

于是可得，三角形APB相似于三角形ABD

于是BP/BD = AB/AD

同理得：CP/CD = AC/AD

又AB=AC

于是BP/BD = CP/CD

即BP*CD = CP*BD

联合上面的托勒密得2BP*CD = 2CP*BD = BC*DP = 2BM*DP

提取BP*CD = BM*DP

即BP/BM = DP/CD

又∠MBP = ∠CDP（同弧所对圆周角相等）

于是三角形MBP相似于三角形CDP

于是结论得证。

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
#include <string>
#define LL long long

using namespace std;

const double PI = acos(-1);

inline double dis(double xA, double yA, double xB, double yB)
{
    double ans = (xA-xB)*(xA-xB) + (yA-yB)*(yA-yB);
    return sqrt(ans);
}

void work()
{
    double xA, yA, xB, yB, xC, yC;
    double a, h, d, ans, v, r;
    scanf("%lf%lf%lf%lf%lf%lf", &xA, &yA, &xB, &yB, &xC, &yC);
    d = dis(xB, yB, xC, yC)/2;
    h = dis(xA, yA, xB, yB);
    a = asin(d/h);
    v = PI-2*a;
    r = h*tan(a);
    ans = sqrt(h*h-d*d)+v*r;
    printf("%.4lf\n", ans);
}

int main()
{
    //freopen("test.in", "r", stdin);
    int T;
    scanf("%d", &T);
    for (int times = 1; times <= T; ++times)
    {
        printf("Case #%d: ", times);
        work();
    }
    return 0;
}

ACM学习历程—HDU5476 Explore Track of Point（平面几何）（2015上海网赛09题）

标签：

原文地址：http://www.cnblogs.com/andyqsmart/p/4857623.html