Binary Heap

标签：

(referrence: cmu_binary_heap)

Definition

A binary heap is a complete binary tree arranged in heap ordering property.

There are two types of ordering:

1. min-heap

The value of each node >= the value of its parent. Root is minimum-value element.

2. max-heap

The value of each node <= the value of its parent. Root is maximum-value element.

Usually, the word "heap" refers to a min-heap.

Example of min-heap

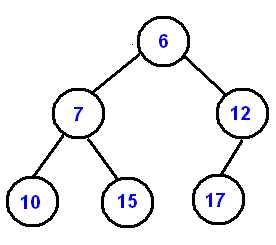
Example of max-heap

Array Implementation

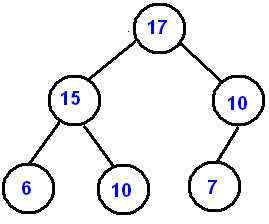
A complete binary tree can be uniquely represented by storing its level order traversal in an array.

We skip the index zero cell of the array for the convenience of implementation. Consider k-th element of the array:

its left child index: 2 * k

its right child index: 2 * k + 1

its parent index: k / 2 

Insert 

The new element is initially appended to the end of the heap (as the last element of the array). The heap property is repaired by comparing the added element with its parent and moving the added element up a level (swapping positions with the parent). 

 1 public void insert(Comparable x)
 2 {
 3     if(size == heap.length - 1) doubleSize();
 4 
 5     //Insert a new item to the end of the array
 6     int pos = ++size;
 7 
 8     //Percolate up
 9     for(; pos > 1 && x.compareTo(heap[pos/2]) < 0; pos = pos/2 )
10         heap[pos] = heap[pos/2];
11 
12     heap[pos] = x;
13 }

Time complexity O(log n) 

DeleteMin

1. Save last element value to root.

2. Decrease heap size by 1.

3. Restore the heap property.

Start from root, do follow steps in a loop until to the bottom:

Switch current (parent) value with smaller one of its two child.

Time complexity O(log n). Details can be checked here. 

FindMin

Return first element.

In Java, PriorityQueue is based on a priority heap. The elements of the priority queue are ordered according to their natural ordering, or by a Comparator provided at queu construction time.

Binary Heap

标签：

原文地址：http://www.cnblogs.com/ireneyanglan/p/4858169.html