标签:
一、编写程序,用对话框显示两个数的加减乘除。
程序代码如下:
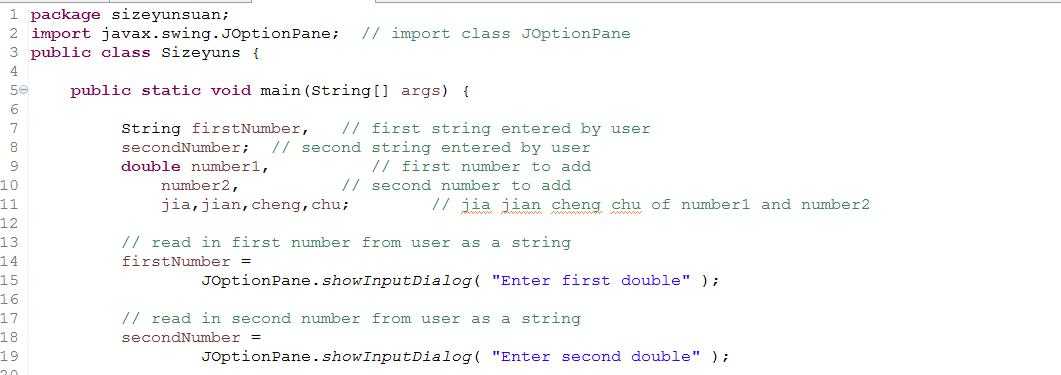
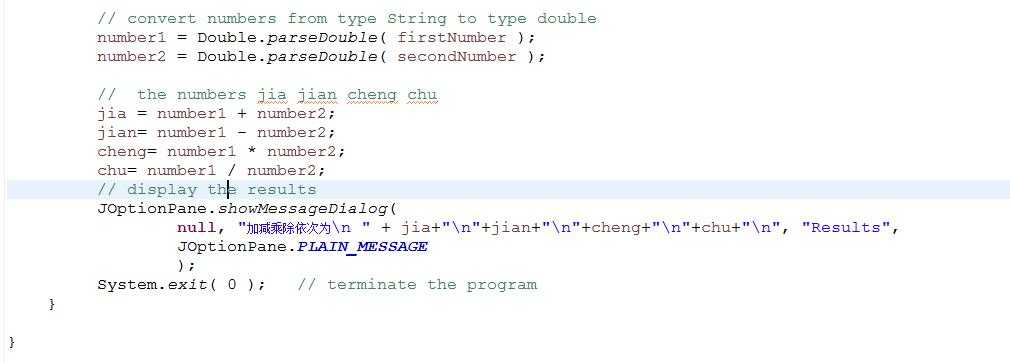
二、运行EnumTest..Java代码,分析运行结果
代码如下:

结果:

分析:枚举类型是引用类型!
枚举不属于原始数据类型,它的每个具体值都引用一个特定的对象。相同的值则引用同一个对象。
可以使用“==”和equals()方法直接比对枚举变量的值,换句话说,对于枚举类型的变量,“==”和equals()方法执行的结果是等价的。
三、反码、补码跟原码概念
原码(true form)是一种计算机中对数字的二进制定点的表示方法。原码是指一个二进制数左边加上符号位后所得到的码,且当二进制数大于0时,符号位为0;二进制数小于0时,符号位为1;二进制数等于0时,符号位可以为0或1。不能直接参加运算。
补码(two‘s complement),在计算机系统中,数值一律用补码来表示和存储。原因在于使用补码,可以将符号位和数值位统一处理;同时,加法和减法也可以统一处理。此外,补码与原码的的相互转换,其运算过程是相同的,不需要额外的硬件电路。
反码表示法规定:正数的反码与其原码相同;负数的反码是对其原码逐位取反,但符号位除外。
四、动手实验TestDouble 代码。
代码如下:

会发现一些问题,结果和我们想的不一样。
为什么Java中用double进行计算会出现精度丢失呢?在查阅了一些资料以后,可知:
首先得从计算机本身去讨论这个问题。我们知道,计算机并不能识别除了二进制数据以外的任何数据。无论我们使用何种编程语言,在何种编译环境下工作,都要先把源程序翻译成二进制的机器码后才能被计算机识别。以上面提到的情况为例,我们源程序里的数字是十进制的,计算机不能直接识别,要先编译成二进制。但问题来了,比如2.4的二进制表示并非是精确的2.4,反而最为接近的二进制表示是2.3999999999999999。原因在于浮点数由两部分组成:指数和尾数,这点如果知道怎样进行浮点数的二进制与十进制转换,应该是不难理解的。如果在这个转换的过程中,浮点数参与了计算,那么转换的过程就会变得不可预 知,并且变得不可逆。我们有理由相信,就是在这个过程中,发生了精度的丢失。而至于为什么有些浮点计算会得到准确的结果,应该也是碰巧那个计算的二进制与十进制之间能够准确转换。
五、运用string进行计算可以解决精度丢失问题
程序代码:
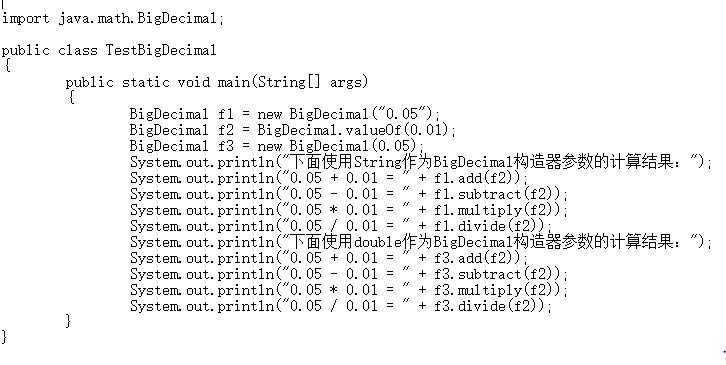
结果
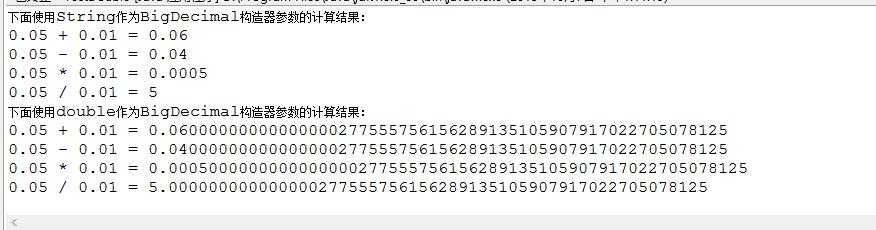
运行此代码可以发现,使用String作为BigDecimal构造器参数结果准确。
在《Effective Java》这本书中给出了一个解决方法。该书中也指出,float和double只能用来做科学计算或者是工程计算,在商业计算等精确计算中,我们要用java.math.BigDecimal。如果需要精确计算,我们不能直接用double,而非要用 String来构造BigDecimal不可!
标签:
原文地址:http://www.cnblogs.com/jinghun/p/4858599.html