标签:
Given numRows, generate the first numRows of Pascal‘s triangle.
For example, given numRows = 5,
Return
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
杨辉三角主要有下列五条性质:
 行的数字个数为
行的数字个数为 个。
个。 行的第
行的第 个数字为组合数
个数字为组合数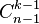 。
。 行数字和为
行数字和为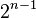 。
。 行第
行第 个数字等于第
个数字等于第 行的第
行的第 个数字与第
个数字与第 个数字的和)。这是因为有组合恒等式:
个数字的和)。这是因为有组合恒等式: 。
。
解法1:根据杨辉三角的构造方法直接构造。
class Solution { public: vector<vector<int>> generate(int numRows) { vector< vector<int> > res; for(int i = 0; i < numRows; i++) { vector<int> row(i + 1, 1); for(int j = 1; j < i; j++) row[j] = res[i - 1][j - 1] + res[i - 1][j]; res.push_back(row); } return res; } };
解法2:杨辉三角的每一行的各元素即是组合数C(m,n),其中n表示第几行,m=0,1,...,n,使用公式C(m,n)=n!/m!/(n-m)!
class Solution { public: vector<vector<int>> generate(int numRows) { vector< vector<int> > res; for(int i = 0; i < numRows; i++) { vector<int> row(i + 1, 1); for(int j = 0; j <= i; j++) row[j] = fact(i) / fact(j) / fact(i - j); res.push_back(row); } return res; } private: long long fact(int n) { if(n <= 1) return 1; long long f = 1, res; for(int i = 2; i <= n; i++) { res = f * i; f = res; } return res; } };
注意这个不能通过全部测试,原因在于numRows比较大时计算阶乘会溢出。考虑组合数计算的另外的公式C(m,n)=C(m-1,n-1)+C(m,n-1)可以改进:
class Solution { public: vector<vector<int>> generate(int numRows) { vector< vector<int> > res; for(int i = 0; i < numRows; i++) { vector<int> row = getRow(i); res.push_back(row); } return res; } private: vector<int> getRow(int rowIndex) { vector<int> row; if (rowIndex < 0) return row; row.assign(rowIndex + 1, 0); for (int i = 0; i <= rowIndex; ++i) { if (i == 0) { row[0] = 1; continue; } for (int j = rowIndex; j >= 1; --j) row[j] = row[j] + row[j - 1]; } return row; } };
这个方法效率比较差,因为为了计算第row行的数据,首先将第1行到第row-1行的所有数据都计算了一遍。
[LeetCode]15. Pascal's Triangle杨辉三角
标签:
原文地址:http://www.cnblogs.com/aprilcheny/p/4859217.html