标签:
There are N children standing in a line. Each child is assigned a rating value.
You are giving candies to these children subjected to the following requirements:
What is the minimum candies you must give?
Key to the problem is to consider the whole array as combination of many ascending sub-arrays and descending sub-arrays. So when we solve candy distribution problems among these sub-arrays, the whole problem is solved.
There are some points to note:
1. To find descending sub-array like 5, 4, 3, 2, 1, we can traverse from right to left. In this way, the sub-array is ascending.
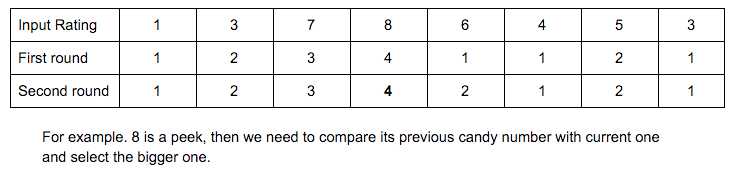
2. For each peek, like 5 in 1, 2, 3, 4, 5, 4, 1, we need compare its previous candy number with current candy number.
Example
1 public class Solution { 2 public int candy(int[] ratings) { 3 if (ratings == null || ratings.length < 1) 4 return 0; 5 int length = ratings.length; 6 if (length == 1) 7 return 1; 8 int[] candyNum = new int[length]; 9 candyNum[0] = 1; 10 int result = 0; 11 int index = 1; 12 // First, process ascending sub-array 13 while (index < length) { 14 if (ratings[index] > ratings[index - 1]) 15 candyNum[index] = candyNum[index - 1] + 1; 16 else 17 candyNum[index] = 1; 18 index++; 19 } 20 21 // Then, process descending sub-array 22 index = length - 2; 23 result = candyNum[length - 1]; 24 while (index >= 0) { 25 if (ratings[index] > ratings[index + 1]) 26 // Here, we need compare 27 candyNum[index] = Math.max(candyNum[index + 1] + 1, candyNum[index]); 28 result += candyNum[index]; 29 index--; 30 } 31 32 return result; 33 } 34 }
标签:
原文地址:http://www.cnblogs.com/ireneyanglan/p/4859955.html