我的递归思路。

标签：

     算法可以说是计算机里的数学，也可以描述成带有计算机特点的数学。我把递归视为一种特别的函数。用数学的思想来思考递归更加明晰快速。

   看一个经常见到的例子，累加1+2+3+4+···········+n。

 数学表达式为：

代码形式为：

	public  int Sum(int n)
	{
	    if(n==1) {return 1;}
	    else {return n+Sum(n-1);}
	}

 这是我们常见的形式，递归出口为: n>1。递归体为: f(n-1)+n。这是一个出口，思考一下，数值为1，2，4,5，，，n，既然n>1可以作为出口 ，数值小于n是否同样可行呢。累加换一种更加普遍问法，n,n+1,n+2,n+3,n+4，，，+m-1,m

这样边界更加清晰。

数学表达式为：

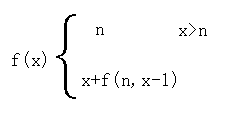
把小的那头作为递归出口。

把大的那头作为递归出口。

代码写出来:

	public  int Sum(int start, int end)
	{
	      if(end==start)  {return start;}
	      else {return end+Sum(start,end-1);}
	}

	public int Sum(int start ,int end)
	{
	    if(start<end) return start+ Sum(start+1,end);
	    else    return end;	
	}

代码按顺序对应。

在看另一个经典范例，斐波那契数列：1,1,2,3,5,8,13,21..........。数学描述为

代码描述为：

	public int fib(int n)
	{
	    if(n==1) return 1;
	    if(n==2) return 1;
	    return fib(n-1)+fib(n-2);
	}

十分明显的对应关系。用数学表达式也很容易描述。然而现实的递归，往往递归体比较复杂，不像例子中的单线递归。多路递归就相当麻烦了。

比如归并排序。二路归并情况下代码

   private  void MergeSortFunction(int[] array, int first, int last)
        {
                if (first < last)  
                {
                    int mid = (first + last) / 2;  
                    MergeSortFunction(array, first, mid);   //对划分出来的左侧子表进行递归划分
                    MergeSortFunction(array, mid + 1, last);    //对划分出来的右侧子表进行递归划分
                    MergeSortCore(array, first, mid, last); //对左右子表进行有序的整合（归并排序的核心部分）
                }
        }

数学描述有些困难，需要动用积分函数的知识，脑补了。二路归并的思路是，层层分割，知道分割成一个个的单元，然后层层配对合并排序，直到最后完成。递归出口是最小单元（即各个数值元素），表现出来就是first=last，无可分割，递归体在递归到出口后一层层返回的过程中一层层排序，直到最后排序完成。

当遇到个问题可分割，分割的结果又存在相似性，有明确的边界条件，并且分割的上一层级对下一层级具有依赖性，就可以考虑递归的使用，仔细考虑，递归边界，边界内的代码，边界外的代码三部分。考虑成熟了，代码也差不多出来了。

我的递归思路。

标签：

原文地址：http://my.oschina.net/hunjixin/blog/514380