标签:
上一周我们研究了2xN的骨牌问题,这一周我们不妨加大一下难度,研究一下3xN的骨牌问题?
所以我们的题目是:对于3xN的棋盘,使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢?
首先我们可以肯定,奇数长度一定是没有办法覆盖的;对于偶数长度,比如2,4,我们有下面几种覆盖方式:
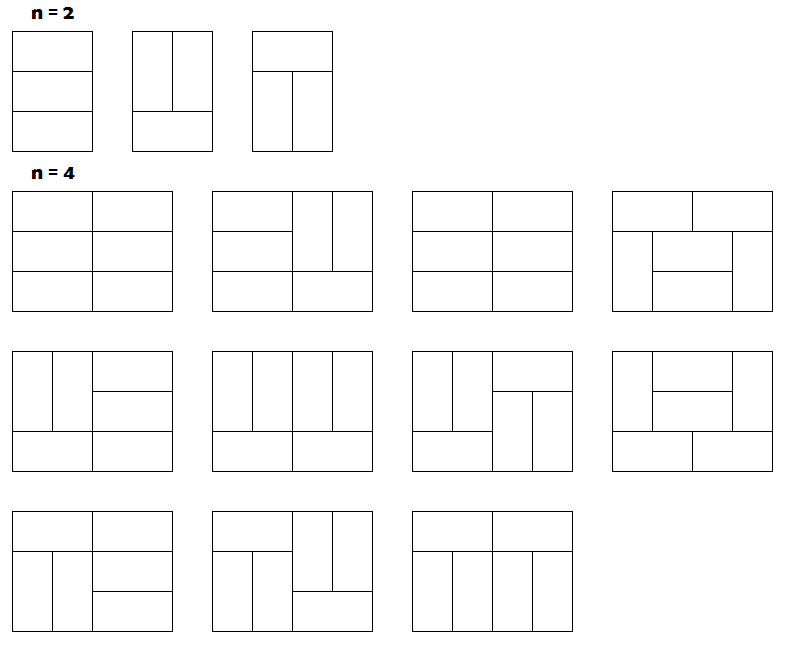
第1行:1个整数N。表示棋盘长度。1≤N≤100,000,000
第1行:1个整数,表示覆盖方案数 MOD 12357
62247088
4037
解题:造转移方程

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const LL mod = 12357; 5 struct Matrix{ 6 int m[8][8]; 7 Matrix(){ 8 init(); 9 } 10 void init(){ 11 memset(m,0,sizeof m); 12 } 13 Matrix operator*(const Matrix &rhs){ 14 Matrix ret; 15 for(int k = 0; k < 8; ++k) 16 for(int i = 0; i < 8; ++i) 17 for(int j = 0; j < 8; ++j) 18 ret.m[i][j] = (ret.m[i][j] + m[i][k]*rhs.m[k][j])%mod; 19 return ret; 20 } 21 void print(){ 22 for(int i = 0; i < 8; ++i){ 23 for(int j = 0; j < 8; ++j) 24 printf("%d ",m[i][j]); 25 cout<<endl; 26 } 27 } 28 }; 29 Matrix a,b; 30 void quickPow(LL index){ 31 while(index){ 32 if(index&1) a = a*b; 33 index >>= 1; 34 b = b*b; 35 } 36 } 37 bool tab[10][10]; 38 void dfs(int cur,int st){ 39 if(cur >= 3){ 40 int ss = 0; 41 for(int i = 2; i >= 0; --i){ 42 ss <<= 1; 43 ss |= tab[i][1]; 44 } 45 b.m[st][ss]++; 46 return; 47 } 48 if(!tab[cur][0]){ 49 if(!tab[cur][1]){ 50 tab[cur][0] = tab[cur][1] = true; 51 dfs(cur+1,st); 52 tab[cur][0] = tab[cur][1] = false; 53 } 54 if(cur + 1 < 3){ 55 if(!tab[cur+1][0]){ 56 tab[cur+1][0] = tab[cur][0] = true; 57 dfs(cur+2,st); 58 tab[cur+1][0] = tab[cur][0] = false; 59 } 60 } 61 }else dfs(cur + 1,st); 62 } 63 void init(int st){ 64 memset(tab,false,sizeof tab); 65 for(int i = 0,xst = st; i < 3; ++i,xst >>= 1) 66 tab[i][0] = xst&1; 67 dfs(0,st); 68 } 69 int main(){ 70 int n; 71 while(~scanf("%d",&n)){ 72 b.init(); 73 a.init(); 74 for(int i = 0; i <= 7; ++i) init(i); 75 a.m[0][0] = 1; 76 quickPow(n); 77 printf("%d\n",a.m[0][0]); 78 } 79 return 0; 80 }
标签:
原文地址:http://www.cnblogs.com/crackpotisback/p/4862273.html