Gradient Boost Decision Tree(&Treelink)

1.      什么是Treelink

      Treelink是阿里集团内部的叫法，其学术上的名称是GBDT（Gradient Boosting Decision Tree，梯度提升决策树）。GBDT是“模型组合+决策树”相关算法的两个基本形式中的一个，另外一个是随机森林（Random Forest），相较于GBDT要简单一些。

1.1    决策树

      应用最广的分类算法之一，模型学习的结果是一棵决策树，这棵决策树可以被表示成多个if-else的规则。决策树实际上是将空间用超平面进行划分的一种方法，每次分割的时候，都将当前的空间一分为二，比如说下面的决策树：

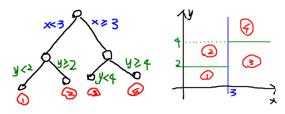
这样使得每一个叶子节点都是在空间中的一个不相交的区域。学习得到如上这棵决策树之后，当输入一个待分类的样本实例进行决策的时候，我们就可以根据这个样本的两个特征（x, y）的取值来把这个样本划分到某一个叶子节点，得到分类结果了，这就是决策树模型的分类过程，决策树的学习算法有ID3算法和C4.5算法等。

 

转自：http://www.cnblogs.com/LeftNotEasy/archive/2011/01/02/machine-learning-boosting-and-gradient-boosting.html

    本来上一章的结尾提到，准备写写线性分类的问题，文章都已经写得差不多了，但是突然听说最近Team准备做一套分布式的分类器，可能会使用Random Forest来做，下了几篇论文看了看，简单的random forest还比较容易弄懂，复杂一点的还会与boosting等算法结合（参见iccv09），对于boosting也不甚了解，所以临时抱佛脚的看了看。说起boosting，强哥之前实现过一套Gradient Boosting Decision Tree（GBDT)算法，正好参考一下。

    最近看的一些论文中发现了模型组合的好处，比如GBDT或者rf，都是将简单的模型组合起来，效果比单个更复杂的模型好。组合的方式很多，随机化（比如random forest），Boosting（比如GBDT）都是其中典型的方法，今天主要谈谈Gradient Boosting方法（这个与传统的Boosting还有一些不同）的一些数学基础，有了这个数学基础，上面的应用可以看Freidman的Gradient Boosting Machine。

    本文要求读者学过基本的大学数学，另外对分类、回归等基本的机器学习概念了解。

    本文主要参考资料是prml与Gradient Boosting Machine。

 

Boosting方法：

    Boosting这其实思想相当的简单，大概是，对一份数据，建立M个模型（比如分类），一般这种模型比较简单，称为弱分类器(weak learner)每次分类都将上一次分错的数据权重提高一点再进行分类，这样最终得到的分类器在测试数据与训练数据上都可以得到比较好的成绩。

   

    上图（图片来自prml p660）就是一个Boosting的过程，绿色的线表示目前取得的模型（模型是由前m次得到的模型合并得到的），虚线表示当前这次模型。每次分类的时候，会更关注分错的数据，上图中，红色和蓝色的点就是数据，点越大表示权重越高，看看右下角的图片，当m=150的时候，获取的模型已经几乎能够将红色和蓝色的点区分开了。

    Boosting可以用下面的公式来表示：

    训练集中一共有n个点，我们可以为里面的每一个点赋上一个权重Wi(0 <= i < n)，表示这个点的重要程度，通过依次训练模型的过程，我们对点的权重进行修正，如果分类正确了，权重降低，如果分类错了，则权重提高，初始的时候，权重都是一样的。上图中绿色的线就是表示依次训练模型，可以想象得到，程序越往后执行，训练出的模型就越会在意那些容易分错（权重高）的点。当全部的程序执行完后，会得到M个模型，分别对应上图的y1(x)…yM(x)，通过加权的方式组合成一个最终的模型YM(x)。

    我觉得Boosting更像是一个人学习的过程，开始学一样东西的时候，会去做一些习题，但是常常连一些简单的题目都会弄错，但是越到后面，简单的题目已经难不倒他了，就会去做更复杂的题目，等到他做了很多的题目后，不管是难题还是简单的题都可以解决掉了。

 

Gradient Boosting方法：

    其实Boosting更像是一种思想，Gradient Boosting是一种Boosting的方法，它主要的思想是，每一次建立模型是在之前建立模型损失函数的梯度下降方向。这句话有一点拗口，损失函数(loss function)描述的是模型的不靠谱程度，损失函数越大，则说明模型越容易出错（其实这里有一个方差、偏差均衡的问题，但是这里就假设损失函数越大，模型越容易出错）。如果我们的模型能够让损失函数持续的下降，则说明我们的模型在不停的改进，而最好的方式就是让损失函数在其梯度（Gradient)的方向上下降。

    下面的内容就是用数学的方式来描述Gradient Boosting，数学上不算太复杂，只要潜下心来看就能看懂：）

    可加的参数的梯度表示：

    假设我们的模型能够用下面的函数来表示，P表示参数，可能有多个参数组成，P = {p0,p1,p2….}，F(x;P)表示以P为参数的x的函数，也就是我们的预测函数。我们的模型是由多个模型加起来的，β表示每个模型的权重，α表示模型里面的参数。为了优化F，我们就可以优化{β,α}也就是P。

    我们还是用P来表示模型的参数，可以得到，Φ(P)表示P的likelihood函数，也就是模型F(x;P)的loss函数，Φ(P)=…后面的一块看起来很复杂，只要理解成是一个损失函数就行了，不要被吓跑了。

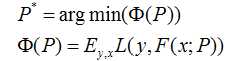   既然模型(F(x;P))是可加的，对于参数P，我们也可以得到下面的式子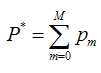：   这样优化P的过程，就可以是一个梯度下降的过程了，假设当前已经得到了m-1个模型，想要得到第m个模型的时候，我们首先对前m-1个模型求梯度。得到最快下降的方向，gm就是最快下降的方向。

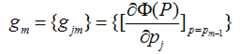    这里有一个很重要的假设，对于求出的前m-1个模型，我们认为是已知的了，不要去改变它，而我们的目标是放在之后的模型建立上。就像做事情的时候，之前做错的事就没有后悔药吃了，只有努力在之后的事情上别犯错：

    我们得到的新的模型就是，它就在P似然函数的梯度方向。ρ是在梯度方向上下降的距离。

    我们最终可以通过优化下面的式子来得到最优的ρ：

    可加的函数的梯度表示：

    上面通过参数P的可加性，得到了参数P的似然函数的梯度下降的方法。我们可以将参数P的可加性推广到函数空间，我们可以得到下面的函数，此处的fi(x)类似于上面的h(x;α)，因为作者的文献中这样使用，我这里就用作者的表达方法：

    同样，我们可以得到函数F(x)的梯度下降方向g(x)

    最终可以得到第m个模型fm(x)的表达式:

 

    通用的Gradient Descent Boosting的框架：

   下面我将推导一下Gradient Descent方法的通用形式，之前讨论过的：

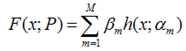    对于模型的参数{β,α}，我们可以用下面的式子来进行表示，这个式子的意思是，对于N个样本点(xi,yi)计算其在模型F(x;α,β)下的损失函数，最优的{α,β}就是能够使得这个损失函数最小的{α,β}。 表示两个m维的参数：

    写成梯度下降的方式就是下面的形式，也就是我们将要得到的模型fm(x)的参数{αm,βm}能够使得fm的方向是之前得到的模型Fm-1(x)的损失函数下降最快的方向：

    对于每一个数据点xi都可以得到一个gm(xi)，最终我们可以得到一个完整梯度下降方向

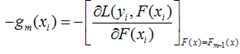    为了使得fm(x)能够在gm(x)的方向上，我们可以优化下面的式子得到，可以使用最小二乘法：

    得到了α的基础上，然后可以得到βm。      最终合并到模型中：

    算法的流程图如下

     之后，作者还说了这个算法在其他的地方的推广，其中，Multi-class logistic regression and classification就是GBDT的一种实现，可以看看，流程图跟上面的算法类似的。这里不打算继续写下去，再写下去就成论文翻译了，请参考文章：Greedy function Approximation – A Gradient Boosting Machine，作者Freidman。

 简单版本：http://www.cnblogs.com/LeftNotEasy/archive/2011/03/07/random-forest-and-gbdt.html

总结：

    本文主要谈了谈Boosting与Gradient Boosting的方法，Boosting主要是一种思想，表示“知错就改”。而Gradient Boosting是在这个思想下的一种函数（也可以说是模型）的优化的方法，首先将函数分解为可加的形式（其实所有的函数都是可加的，只是是否好放在这个框架中，以及最终的效果如何）。然后进行m次迭代，通过使得损失函数在梯度方向上减少，最终得到一个优秀的模型。值得一提的是，每次模型在梯度方向上的减少的部分，可以认为是一个“小”的或者“弱”的模型，最终我们会通过加权(也就是每次在梯度方向上下降的距离）的方式将这些“弱”的模型合并起来，形成一个更好的模型。

    有了这个Gradient Descent这个基础，还可以做很多的事情。也在机器学习的道路上更进一步了：）

1.4    Treelink模型

      Treelink不像决策树模型那样仅由一棵决策树构成，而是由多棵决策树构成，通常都是上百棵树，而且每棵树规模都较小（即树的深度会比较浅）。模型预测的时候，对于输入的一个样本实例，首先会赋予一个初值，然后会遍历每一棵决策树，每棵树都会对预测值进行调整修正，最后得到预测的结果:

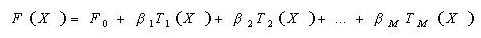
F0是设置的初值， Ti是一棵一棵的决策树。对于不同的问题（回归问题或者分类问题）以及选择不同的损失函数，初值的设定是不同的。比如回归问题并且选择高斯损失函数，那么这个初值就是训练样本的目标的均值。

Treelink自然包含了boosting的思想：将一系列弱分类器组合起来，构成一个强分类器。它不要求每棵树学到太多的东西，每颗树都学一点点知识，然后将这些学到的知识累加起来构成一个强大的模型。

Treelink模型的学习过程，就是多颗决策树的构建过程。在树的构建过程中，最重要的就是寻找分裂点（某个特征的某个取值）。在Treelink算法我们通过损失函数的减小程度用来衡量特征分裂点的样本区分能力，Loss减小得越多，分裂点就越好。即以某个分裂点划分，把样本分成两部分，使得分裂后样本的损失函数值减小的最多。

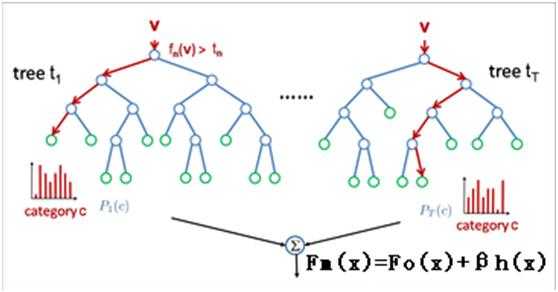
Treelink训练：
1.估算初值；

2.按如下方式创建M棵树：

–更新全部样本估计值；

–随机选取一个样本子集；

–按如下方式创建J个叶子；

•对当前所有叶子

–更新估计值、计算梯度、最优划分点、最优增长量以及增益（损失函数减少量）；

–选择增益最大的叶子及其划分点，进行分裂，同时分裂样本子集；

–将增长量刷新到叶子；

Treelink预测：

将目标估计值赋估值；

•对M棵树：

–根据输入数据的特征（x），按照决策树的路径查找到叶子节点；

–用叶子节点上的增长量更新目标估计值；

•输出结果；

例如，GBDT得到了三棵决策树，一个样本点在预测的时候，也会掉入3个叶子节点上，其增益分别为（假设为3分类的问题）：

(0.5, 0.8, 0.1),  (0.2, 0.6, 0.3),  (0.4, 0.3, 0.3)，

那么这样最终得到的分类为第二个，因为选择分类2的决策树是最多的。

2.      Treelink二元分类性能测试

2.1 实验目的及数据准备

      利用成交情况历史数据，通过treelink预测某个卖家的成交情况，即是否有成交，转化为二元分类问题。

数据格式: target feature1 feature2 … feature13,其中target只有两个值：0代表无成交，1代表有成交，0代表没有成交，每个sample由13个feature进行描述。在样本数据中，正例（target=1）样本数为23285，负例样本数为20430，比率为1.14:1。所有样本数据被分到训练集和测试集两个集合：训练集包括33715个样本，测试集包括10000个样本。

2.2 模型参数设置

      测试环境利用MLLib 1.2.0工具包中的Treelink模块进行，主要工作是在训练过程中根据损失函数的下降趋势和预测准确率对treelink的各项参数进行调节，最终找到一个最优的参数组合。涉及到的配置文件包括：

mllib.conf:

[data]

filter=0

sparse=0

weighted=0

[model]

cross_validation=0

evaluation_type=3

variable_importance_analysis=1

cfile_name=

model_name=treelink

log_file=日志文件保存路径

model_file=模型文件保存路径

param_file=treelink配置文件保存路径

data_file=样本数据文件保存路径

result_file=分类结果文件保存路径

 

treelink.conf:

[treelink]

tree_count=500

max_leaf_count=4

max_tree_depth=4

loss_type=logistic

shrinkage=0.15

sample_rate=0.66

variable_sample_rate=0.8

split_balance=0

min_leaf_sample_count=5

discrete_separator_type=leave_one_out

fast_train=0

tree_count：决策树的个数，越大学习越充分，但太大也会造成过度拟合，而且也消耗训练和预测的时间。可以先选择比较大的树个数，然后观察训练过程中的损失减少趋势，损失减少比较平缓时，树个数就比较合适了。tree_count和shrinkage也有关系，shrinkage越大，学习越快，需要的树越少。
shrinkage：步长，代表学习的速度，越小表示学习越保守（慢），越大则表示学习越冒进（快）。通常可以把Shrinkage设小一点，把树的个数设大一点。
sample_rate：样本采样率，为了构造具有不同倾向性的模型，需要使用样本的子集来进行训练，过多的样本会造成更多的过拟合和局部极小问题。这个采样的比例一般选择50%-70%比较合适。
variable_sample_rate：特征采样率，是指从样本的所有特征中选取部分的特征来学习，而不使用全部特征。当发现训练出来的模型，某一两个特征非常强势，重要性很大，而造成其他特征基本学不到的时候，可以考虑设置一下把这个参数设置成<1的数。

loss_type:设置该参数的时候要格外注意，务必要使优化目标与损失函数保持一致，否则损失函数在训练过程中不但不减小，反而会增大。

其他参数的详细含义可以参见mlllib user manual。

2.3 实验结果

本次试验利用Lift，F_1和AUC三个指标对treelink模型的分类性能进行评估。

Lift：该指标衡量的是与不利用模型相比，模型的“预测”能力变好了多少。模型的lift（提升指数）越大，模型的运行效果更好。Lift=1表示模型没有任何提升。

F_1：是覆盖率与准确率的综合指标，随着precision和coverage的同时增大而增大，公式如下： 

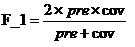
AUC：Area Under ROCCurve，其值等于ROC曲线下的面积，介于0.5到1之间。较大的AUC代表了较好的performance。关于AUC的计算有多种方法，本实验中采用的方法如下： 

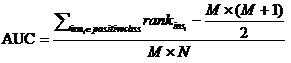
设正例样本数为M，负例样本数为N，样本数n=M+N。首先对score从大到小排序，然后令最大score对应的sample的rank为n，第二大score对应的sample的rank为n-1，以此类推。然后把所有的正例样本的rank值相加，再减去正例样本的score为最小的那M个值的情况。得到的就是所有样本中有多少正例样本的score大于负例样本的score，最后除以M×N。需要特别注意的地方是，在存在score相等的情况时，需要赋予相同的rank值，具体操作是把所有这些score相同的样本的rank取平均。

注：Lift，F_1，ROC曲线可以通过R语言环境机器学习包求得，AUC的计算没有找到常用工具，因此利用python编程实现。

 

模型评估结果：

AUC=0.9999，Lift=1.9994，F_1=0.9999

注：以上评估结果为经过长时间参数调整后treelink的分类性能，结果过于理想，目前尚不能判断是否出现过拟合，需在利用其它数据经过多次实验后方能验证。

Gradient Boost Decision Tree(&Treelink)

标签：

原文地址：http://www.cnblogs.com/zhizhan/p/4868544.html