标签:
题目及解题代码存于此处以便研读
在 Warcraft III 之冰封王座中,毁灭者是不死族打三本后期时的一个魔法飞行单位。
毁灭者的核心技能之一,叫做魔法吸收(Absorb Mana):
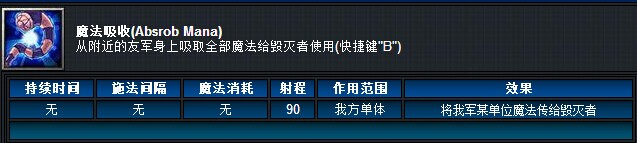
现在让我们来考虑下面的问题:
假设你拥有 n 个魔法单位,他们从左到有站在一行,编号从 1 到 n。 每个单位拥有三项属性:
si: 初始法力。
mi: 最大法力上限。
ri: 每秒中法力回复速度。
现在你操纵一个毁灭者,有 m 个操作,t l r,表示时刻 t,毁灭者对所有编号从 l 到 r 的单位,使用了魔法吸收。操作按照时间顺序给出,计算毁灭者一共吸收了多少法力。
输入数据的第一行有一个整数 n(1 ≤ n ≤105) — 你的魔法单位的数目。
接下来的 n 行,每行有三个整数 si, mi, ri(0 ≤ si ≤ mi ≤ 105, 0 ≤ ri ≤ 105) 描述一个魔法单位。
接下来一行又一个整数 m(1 ≤ m ≤ 105), — 操作的数目。
接下来的 m 行,每行描述一个操作 t, l, r(0 ≤ t ≤ 109, 1 ≤ l ≤ r ≤ n),t 非降。
输出一行一个整数表示毁灭者一共吸收了多少法力。
5 0 10 1 0 12 1 0 20 1 0 12 1 0 10 1 2 5 1 5 19 1 5
83
AC的代码

1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h> 4 #include <iostream> 5 #include <algorithm> 6 #include <vector> 7 #include <map> 8 #include <set> 9 #include <queue> 10 #include <bitset> 11 #include <string> 12 #define PQ priority_queue 13 #define OO 2147483647 14 #define Max(a, b) ((FASTBUFFER = ((a) - (b)) >> 31), ((b) & FASTBUFFER | (a) & ~FASTBUFFER)) 15 #define Min(a, b) ((FASTBUFFER = ((a) - (b)) >> 31), ((a) & FASTBUFFER | (b) & ~FASTBUFFER)) 16 #define Swap(a, b) (a ^= b, b ^= a, a ^= b) 17 18 using namespace std; 19 20 const int N = 100005; 21 22 typedef long long ll; 23 24 inline int ran() { 25 static int x = 1; 26 x += (x << 1) + 1; 27 return x & 2147483647; 28 } 29 30 struct Node; 31 32 typedef pair <Node*, Node*> Pair; 33 34 Node *null; 35 36 struct Node { 37 int val, snow, size; 38 ll sum; 39 Node *left, *right; 40 41 Node (int val, int snow, Node *left, Node *right) : 42 val(val), snow(snow), size(snow), left(left), right(right), sum((ll)val * snow) {} 43 44 Node *Update() { 45 size = left->size + snow + right->size; 46 sum = left->sum + (ll)val * snow + right->sum; 47 return this; 48 } 49 50 Pair split(int v); 51 }; 52 53 Node *Merge(Node *a, Node *b) { 54 if (a == null) { 55 return b; 56 } 57 58 if (b == null) { 59 return a; 60 } 61 62 if (ran() % (a->size + b->size) < a->size) { 63 a->right = Merge(a->right, b); 64 return a->Update(); 65 } 66 67 b->left = Merge(a, b->left); 68 return b->Update(); 69 } 70 71 Pair Node :: split(int v) { 72 if (this == null) { 73 return make_pair(null, null); 74 } 75 76 if (val >= v) { 77 Pair ret = left->split(v); 78 left = ret.second; 79 return make_pair(ret.first, this->Update()); 80 } 81 82 Pair ret = right->split(v); 83 right = ret.first; 84 return make_pair(this->Update(), ret.second); 85 } 86 87 Node *root; 88 89 struct monsterNode { 90 int s, m, r; 91 }a[N]; 92 93 int n, m; 94 ll ans; 95 multiset <int> s; 96 vector <int> listInsert[N], listErase[N]; 97 98 void insertWithTreap(int v) { 99 Pair ret1 = root->split(v), ret2 = ret1.second->split(v + 1); 100 if (ret2.first->size) { 101 ret2.first->snow++; 102 ret2.first->size++; 103 ret2.first->sum += ret2.first->val; 104 root = Merge(ret1.first, Merge(ret2.first, ret2.second)); 105 return; 106 } 107 108 root = Merge(ret1.first, Merge(new Node(v, 1, null, null), ret2.second)); 109 } 110 111 void eraseWithTreap(int v) { 112 Pair ret1 = root->split(v), ret2 = ret1.second->split(v + 1); 113 if (ret2.first->size > 1) { 114 ret2.first->snow--; 115 ret2.first->size--; 116 ret2.first->sum -= ret2.first->val; 117 root = Merge(ret1.first, Merge(ret2.first, ret2.second)); 118 return; 119 } 120 121 root = Merge(ret1.first, ret2.second); 122 } 123 124 void insertQuery(int t) { 125 multiset <int> :: iterator it1 = s.lower_bound(t), it2 = s.upper_bound(t); 126 if (*it1 == t) { 127 s.insert(t); 128 return; 129 } 130 131 if (it1 != s.begin()) { 132 it1--; 133 } else { 134 it1 = s.end(); 135 } 136 137 if (it1 != s.end() && it2 != s.end()) { 138 eraseWithTreap(*it2 - *it1); 139 } 140 141 if (it1 != s.end()) { 142 insertWithTreap(t - *it1); 143 } 144 145 if (it2 != s.end()) { 146 insertWithTreap(*it2 - t); 147 } 148 149 s.insert(t); 150 } 151 152 void eraseQuery(int t) 153 { 154 s.erase(s.find(t)); 155 multiset <int> :: iterator it1 = s.lower_bound(t), it2 = s.upper_bound(t); 156 if (*it1 == t) { 157 return; 158 } 159 160 if (it1 != s.begin()) { 161 it1--; 162 } else { 163 it1 = s.end(); 164 } 165 166 if (it1 != s.end() && it2 != s.end()) { 167 insertWithTreap(*it2 - *it1); 168 } 169 170 if (it1 != s.end()) { 171 eraseWithTreap(t - *it1); 172 } 173 174 if (it2 != s.end()) { 175 eraseWithTreap(*it2 - t); 176 } 177 } 178 179 void askQuery(int start, int m, int r) 180 { 181 if (s.empty()) 182 return; 183 ans += min((ll)(*s.begin()) * r + start, (ll)m); 184 if (r == 0) { 185 return; 186 } 187 188 int full = m / r + ((m % r) > 0); 189 Pair ret = root->split(full); 190 ans += (ll)m * ret.second->size; 191 ans += ret.first->sum * r; 192 root = Merge(ret.first, ret.second); 193 } 194 195 int main() { 196 null = new Node(0, 0, null, null); 197 root = null; 198 scanf("%d", &n); 199 for (int i = 1; i <= n; i++) { 200 scanf("%d %d %d", &a[i].s, &a[i].m, &a[i].r); 201 } 202 203 scanf("%d", &m); 204 for (int i = 1; i <= m; i++) { 205 int t, l, r; 206 scanf("%d %d %d", &t, &l, &r); 207 listInsert[l].push_back(t); 208 listErase[r].push_back(t); 209 } 210 211 for (int i = 1; i <= n; i++) { 212 for (int j = 0; j < listInsert[i].size(); j++) { 213 insertQuery(listInsert[i][j]); 214 } 215 216 askQuery(a[i].s, a[i].m, a[i].r); 217 for (int j = 0; j < listErase[i].size(); j++) { 218 eraseQuery(listErase[i][j]); 219 } 220 } 221 222 cout << ans << endl; 223 return 0; 224 }
标签:
原文地址:http://www.cnblogs.com/AdonisGe/p/4868648.html