标签:
关联分析是一种在大规模数据集中寻找有趣关系的任务,这些关系有两种形式:频繁项集和关联规则。频繁项集是经常出现在一起的物品的集合,关联规则暗示两种物品之间可能存在的很强的关系。
如何寻找数据集中的频繁或关联关系呢?主要是通过支持度和可信度。
一个项集的支持度被定义为数据集中包含该项集的记录所占的比例。
可信度是针对关联规则来定义的,比如规则A->B的可信度为:支持度{A,B} / 支持度{A}
支持度和可信度是用来量化关联分析是否成功的方法。
Apriori原理:
要计算某个项集在数据集的支持度,需要大量的计算。一个有N个数据的集合共有2N-1种项集的组合,即N=100的数据集可能有2100-1中项集的组合,对于普通的计算机而言,需要很长的时间才能完成运算。
为了降低所需的计算时间,通常采用采用Apriori原理,来减少可能感兴趣的项集。
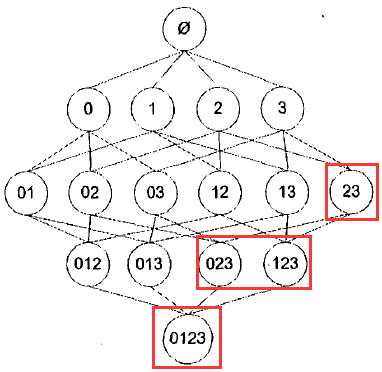
Apriori在拉丁语中指“来自以前”, Apriori原理:如果某个项集是频繁的,那么它的所有子集也是频繁的;如果一个项集是非频繁集,那么它的所有超集也是非频繁的。
比如,一旦计算出{2,3}的支持度,知道它是非频繁的项集,则可推出{1,2,3},{0,2,3}等包含{2,3}的项集也是非频繁的,就不需要再进行计算支持度了。
使用该原理就可以避免项集数据的指数增长,从而在合理的时间内计算出频繁项集。
使用Apriori算法来发现频繁集:
def loadDataSet(): return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]] def createC1(dataSet): C1 = [] for transaction in dataSet: for item in transaction: if not [item] in C1: C1.append([item]) C1.sort() return map(frozenset, C1)#use frozen set so we #can use it as a key in a dict def scanD(D, Ck, minSupport): ssCnt = {} for tid in D: for can in Ck: if can.issubset(tid): if not ssCnt.has_key(can): ssCnt[can]=1 else: ssCnt[can] += 1 numItems = float(len(D)) retList = [] supportData = {} for key in ssCnt: support = ssCnt[key]/numItems if support >= minSupport: retList.insert(0,key) supportData[key] = support return retList, supportData def aprioriGen(Lk, k): #creates Ck retList = [] lenLk = len(Lk) for i in range(lenLk): for j in range(i+1, lenLk): L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2] L1.sort(); L2.sort() if L1==L2: #if first k-2 elements are equal retList.append(Lk[i] | Lk[j]) #set union return retList def apriori(dataSet, minSupport = 0.5): C1 = createC1(dataSet) D = map(set, dataSet) L1, supportData = scanD(D, C1, minSupport) L = [L1] k = 2 while (len(L[k-2]) > 0): Ck = aprioriGen(L[k-2], k) Lk, supK = scanD(D, Ck, minSupport)#scan DB to get Lk supportData.update(supK) L.append(Lk) k += 1 return L, supportData
标签:
原文地址:http://www.cnblogs.com/zhq1007/p/4848425.html