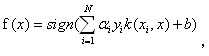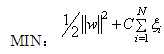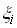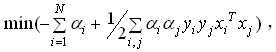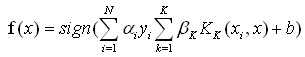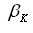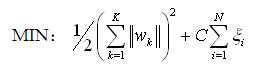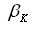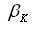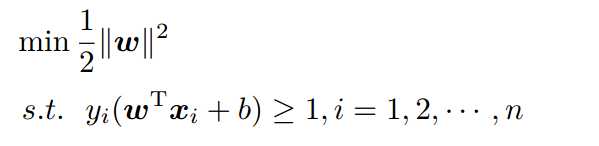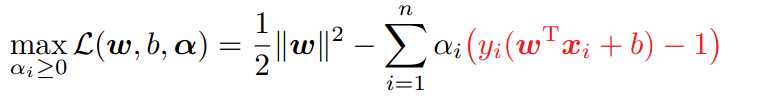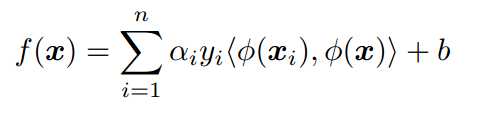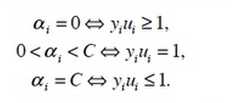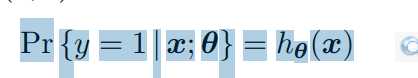SVM
1.
普通SVM的分类函数可表示为:
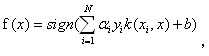
其中ai为待优化参数,物理意义即为支持向量样本权重,yi用来表示训练样本属性,正样本或者负样本,为计算内积的核函数,b为待优化参数。
其优化目标函数为:
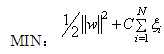
其中||w||用来描述分界面到支持向量的宽度,越大,则分界面宽度越小。C用来描述惩罚因子,而
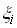
则是用来解决不可分问题而引入的松弛项。
在优化该类问题时,引入拉格朗日算子,该类优化问题变为:
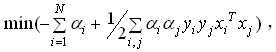
其中待优化参数ai在数学意义上即为每个约束条件的拉格朗日系数。
而MKL则可认为是针对SVM的改进版,其分类函数可描述为:
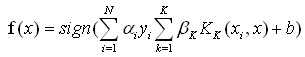
其中,Kk(xi,x)表示第K个核函数,
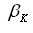
则为对应的核函数权重。
其对应的优化函数可以描述为:
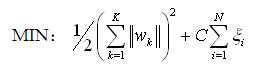
在优化该类问题时,会两次引入拉格朗日系数,ai参数与之前相同,可以理解为样本权重,而
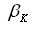
则可理解为核函数的权重,其数学意义即为对每个核函数引入的拉格朗日系数。具体的优化过程就不描述了,不然就成翻译论文啦~,大家感兴趣的可以看后面的参考文档。
通过对比可知,MKL的优化参数多了一层
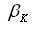
其物理意义即为在该约束条件下每个核的权重。
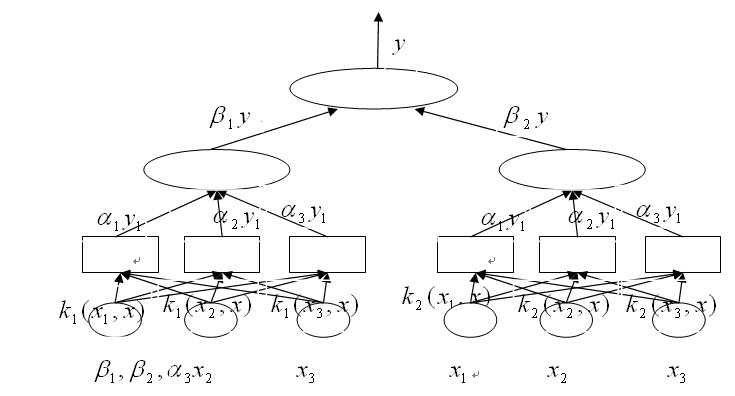
Svm的分类函数形似上是类似于一个神经网络,输出由中间若干节点的线性组合构成,而多核学习的分类函数则类似于一个比svm更高一级的神经网络,其输出即为中间一层核函数的输出的线性组合。其示意图如下:
上图中,左图为普通SVM示例,而全图则为MKL示例。其中
2.
- 通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。对超平面中参数w和b 的求解,最后转换成了对偶因子的求解,总体思路就是:从最大间隔出发(目的本就是为了确定法向量w),转化为求对变量w和b的凸二次规划问题。
- 求分类函数f(x) =w· x+b 的问题转化到求最大分类间隔,继而再转化为对w、b 的最优化问题,即凸二次规划问题,妙
- 超平面(w,b) 关于训练数据集T的函数间隔为超平面(w,b) 关于T中所有样本点(xi,yi) 的函数间隔最小值,但是同比例增大w和b,函数间隔将变大,但是平面还是不变的,所以就将函数间隔变为几何间隔(函数间隔/|w|),可以认为函数间隔为人为定义的一个间隔度量,几何间隔为真正到超平面的距离,所以SVM算法就是最大化最小几何距离,因为说了函数间隔相当于是人为定义的一个间隔,所以最小的函数间隔可以定义为1,那么支持向量的函数间隔就为1(支持向量满足y(wx+b)=1),对于其他不是支持向量的点有y(wx+b)>1
- 支持向量不一定只有两个,可以大于等于2个支持向量
- 原始问题的最优化的问题变为了
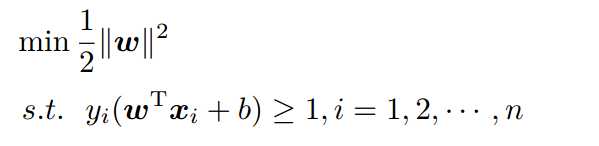
这是一个二次优化问题(QP)(目标函数是二次的,约束条件是一次的),通过Lagrange对偶变换到对偶变量的优化问题
引入对偶问题的优点:对偶问题更容易求解,可以自然引入核函数,进而推广到非线性分类问题,直接处理不等式的约束是很困难的
- 关于什么是Lagrange对偶性?简单地来说,通过给每一个约束条件加上一个Lagrange乘
子,即引入Lagrange对偶变量
,如此我们便可以通过Lagrange函数将约束条件融和到目标函数里去(也就
是说把条件融合到一个函数里头,现在只用一个函数表达式便能清楚的表达出我们的问题)
- 核函数可以学习非线性支持向量机,等价于隐式地在高位的特征空间中学习线性支持向量机,这样的方法称之为核技巧
- y(wx+b)表示分类的正确性和确信度
- 由于支持向量在确定分离超平面中起着决定性作用,所以将这种分类模型称之为支持向量机,支持向量的个数一般很少,所以支持向量由很少的“重要的”训练样本决定
- 对于近似线性可分的w的解释唯一的,但是b 的解不是唯一的,是存在于一个范围内的,但是对于硬支持向量机时w和b 的解是唯一的
- 对于软间隔的支持向量xi或者在间隔边界上,或者在间隔边界与分离超平面之间,或者在分离超平面误分的一侧,若a*i<C,支持向量 xi恰好落在间隔边界上,若a*i=C,0<§<1,则分类正确,xi在间隔超平面与分离超平面之间,若a*i=c,§i=1,则xi在分离超平面上,若a*i=c,§i>1,则xi位于分离超平面误分的一侧
- 核技巧的思想:在学习和预测中只定义核函数K(X,Z),而不显示的定义映射函数,通常计算K(X,Z)比较容易,计算映射函数然后计算核函数不容易,对于给定的核函数,特征空间H和银蛇函数的取法并不唯一,可以取不同的特征空间,对于同一特征空间也可以取不同的映射,学习是隐式在特征空间进行的,不需要显示地定义特征空间和映射函数,这样的技巧称为核技巧
- 通常所说的核函数都是正定核函数
- 对于线性可分的支持向量机称为LSVM
- 在求对偶问题的时候,经常会遇到最大最小问题,因此这里maxmin<=minmax的解,这是因为最小值中最大值是小于最大值中的最小值的
- 为什么对于非支持向量ai是等于0的,就是这些“后方”的点——正如我们之前分析过的一样,对超平面是没有影响的,由于分类完全有超平面决定,所以这些无关的点并不会参与分类问题的计算,因而也就不会产生任何影响了
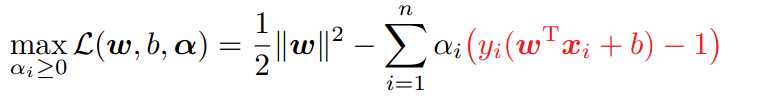
注意到如果xi 是支持向量的话,(2.1.23)式中红颜色的部分是等于0的(因为支持向量的函数间隔等于1),而对于非支持向量来说,函数间隔会大于1,因此红颜色部分是大于零的,而αi 又是非负的,为了满足最大化,αi
必须等于0。这也就是这些非支持向量的点的局限性
支持向量机的处理方法是选择一个核函数κ(·,·),通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。由于核函数的优良品质,这样的非线性扩展在计算量上并没有比原来复杂多少,这一点是非常难得的
支持向量机的分类函数的特性:它是一组以支持向量为参数的非线性函数的线性组合,因此分类函数的表达式仅和支持向量的数量有关,而独立于空间的维度,在处理高维输入空间的分类时,这种方法尤其有
效,因为对于非支持向量,其对应的系数ai=0;
如果没有核函数这一概念,那么就需要找那么映射将低维空间的向量映射到高维空间,这个函数一般不太容易找到,而且增加了编程的难度,代码的可复用性就小,映射到高纬的数据有可能造成维数灾难,所以这样并不是一个好方法,而对于使用了核函数的,
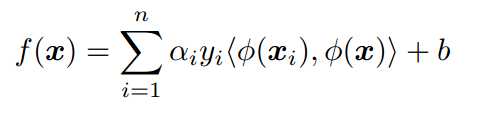
其中只需要??(xi), ?(x)?代替<xi,xj>内积的部分,这样可以使得代码的可复用性好,直接从线性推广到非线性的部分
核函数避免直接在高维空间进行计算, 结果确是等价的
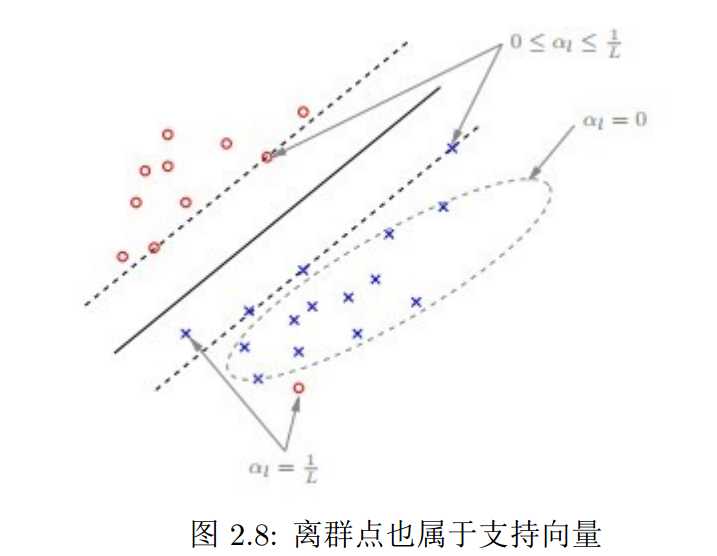
- 对于非线性分类器的理解:在有松弛的情况下,离群点也属于支持向量,对于不同的支持向量,Lagrange参数的值也是不同的,对于离群点,如果把它移动回来,就刚好落在原来的分割平面上了(通过移动后的数据,如果落在分割平面上就属于支持向量,(这是我自己的理解)),而不是的超平面发生变形
- 对于不同的支持向量,Lagrange参数的值也不同,如此篇论文“Large Scale
Machine Learning”中图所示(图2.8),对于远离分类平面的点值为0;对于边缘上的点值在[0,1/L] 之间,其中,L为训练数据集个数,即数据集大小;对于离群点和内部的数据值为1/L
- 对于线性支持向量,有一个概念需要想清楚就是其中�是需要优化的变量(之一),而C是一个事先确定好的常量
- 在支持向量机中ai的取值的意义:
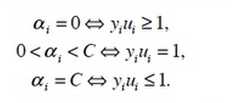
- 其中第一个表达式表示ai是正常分类,在边界内部
- 第二个表达式表明ai是支持向量,在边界上
- 都三种情况表示ai在两条边界之间
- 其解释的过程如下:

3.在逻辑回归中,
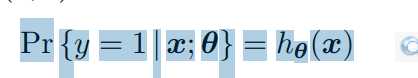
看做为对于x,输出y=1的概率,1-h(x)为y=0的概率,当h(x)>=0.5的时候就是y=1的类,反之就是y=0的类