标签:
科学记数法
把一个绝对值小于1(或者大于等于10)的实数记为a×10n的形式(其中1≤/a/<10),这种记数法叫做科学记数法。
这是一种记数的方法。把一个绝对值小于1(或者大于等于10)的实数记为a×10^n的形式(其中1≤|a|<10),这种记数法叫做科学记数法。例如19971400000000=1.99714×10^13。计算器或电脑表达10的的幂是一般是用E或e,也就是1.99714E13=19971400000000。
当我们要标记或运算某个较大或较小且位数较多时,用科学记数法免去浪费很多空间和时间。
科学记数法的形式是由两个数的乘积组成的。表示为a×10^b(aEb)
其中一个因数为a(1≤|a|<10),另一个因数为10^n(n是比A的整数部分少1的正整数)。
用科学记数法表示数时,不改变数的符号,只是改变数的书写形式而已。可以方便的表示日常生活中遇到的一些极大或极小的数,如:光的速度大约是300,000,000米/秒;全世界人口数大约是:6,100,000,000.
这样的数,读、写都很不方便,我们可以免去写这么多重复的0,将其表现为这样的形式:6,100,000,000=6.1×10^9,
或:0.00001=1×10^-5,即绝对值小于1的数也可以用科学记数法表示为a乘10 的负n次方的形式。
一般地,将绝对值大于1的数字  记为:
记为: 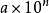 的形式,
的形式,  的值由
的值由  的位数决定,
的位数决定,  为
为 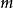 位数,则
位数,则 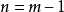 ,
,
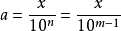
如果  是绝对值小于1的数字,且有
是绝对值小于1的数字,且有 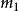 位有效数字,则
位有效数字,则 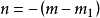 ,
, 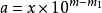
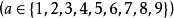
精确度
运用科学记数法a×10^n的数字,它的精确度以a的最后一个数在原数中的数位为准。
如:1.32X10^4,精确到百位
320200,精确到千位,记作:3.20X10^5
aEb=a×10^b
1. 3×10^4+4×10^4=7×10^4
即aEc±bEc=﹙a±b﹚Ec
2. 3E6×6E5=1.8E11
即aEM×bEN=abE(M+N)
3. -6E4÷3E3=-2E1
即aEM÷bEN=a/bE(M-N)⑷
相关的一些推导
(aEc)^2=(aEc)(aEc)=a^2E2c
(aEc)^3=(aEc)(aEc)(aEc)=a^3E3c
(aEc)^n=a^nEnc
a×10^logb=ab
aElogb=ab
⒍n"E"公式 3E4E5=30000E5=3E9
即aEbEc=aEb+c
6E-3E-6E3=0.006E-6E3
=0.000000006E3
=6E-6
即aEbEcEd=aEb+c+d
得aEa1Ea2Ea3.......Ean=aEa1+a2+a3+.......+an
⒎n"E"公式与数列
据n"E"公式aEa1Ea2Ea3.......Ean=aEa1+a2+a3+.......+an
得aESn
等差n项和公式na1+n(n+1)/2×d
aEna1+n(n+1)/2×d
等比n项和公式Sn=a1n(q=1)或 n(1-q^n)/1-q
aESn [Sn=a1n(q=1)或 n(1-q^n)/1-q(q≠1) ]
数列通项记数
等差:aEan=aEa1+(n-1)d
等比:aEan=aEa1q^n-1
⒏aEb与aE-b
aEb=a×10^b
aE-b=a×10^-b 正负b决定E的方向
科学记数意义
"aE"表示并非具有科学记数意义,并且aE=a
"Ea"表示具有科学记数意义,即Ea=1Ea a=3时 1E3=1000
aEb=c a=c/Eb
标签:
原文地址:http://www.cnblogs.com/Chary/p/No000012.html