杭电ACM 2036 改革春风吹满地

标签：blog   http   os   art   io   for   

已知直角坐标系3点p(a,b),m(c,d),n(e,f) 求三角形pmn面积的表达式！ 

解：

无论三角形的顶点位置如何，△PMN总可以用一个直角梯形（或矩形）和两个直角三角形面积的和差来表示
而在直角坐标系中，已知直角梯形和直角三角形的顶点的坐标，其面积是比较好求的。
下面以一种情形来说明这个方法，其它情形方法一样，表达式也一样（表达式最好加上绝对值，确保是正值）
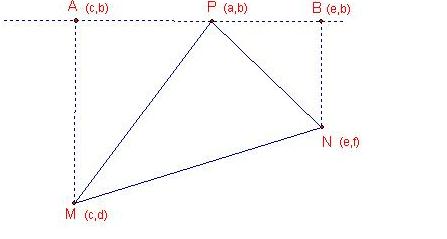
如图情形（P在上方，M在左下，N在右下），过P作X轴的平行线L，作MA⊥L，NB⊥L（设P在A、B之间）
则A、B的坐标是A(c,b)，B(e,b)
所以PA＝a－c,PB＝e－a,AM＝b－d,BN＝b－f,AB＝e－c
所以S△PMN＝S梯形AMNB－S△PAM－S△PBN
＝(b－d＋b－f)(e－c)/2－(b－d)(a－c)/2－(b－f)(e－a)/2
＝(ad＋be＋cf－af－bc－de)/2

 

即：

三角形三顶点坐标分别为A(a,b),B(c,d),C(e,f)，那么这个三角形的面积为
S=1/2*三阶行列式，

三阶行列式为：

a  b  1

c  d  1

e  f  1

#include <iostream>
#include <iomanip>
using namespace std;
int x[100],y[100];
float s(int a,int b,int c,int d,int e,int f){
return (a*d+c*f+b*e-e*d-c*b-a*f)/2.0;
}
int main()
{
int n;
while(cin>>n&&n!=0){
float res=0;
for(int i=0;i<n;i++)
cin>>x[i]>>y[i];
for(int i=0;i<n-2;i++){
//triangle
res=res+s(x[0],y[0],x[i+1],y[i+1],x[i+2],y[i+2]);
}
printf("%.1f\n",res);
}
return 0;
}

杭电ACM 2036 改革春风吹满地,布布扣,bubuko.com

杭电ACM 2036 改革春风吹满地

标签：blog   http   os   art   io   for   

原文地址：http://www.cnblogs.com/tyx0604/p/3851372.html