标签:
2.多边形
(polygon.pas/c/cpp)
【问题描述】
在平面直角坐标系中给出一个顶点横纵坐标均为整数的简单多边形[1],求在这个多边形内部有多少个横纵坐标均为整数的点。
【输入】
输入文件名为polygon.in,共 行,第一行包含一个正整数 。
下面共 行,每行包含两个整数 ,依次表示多边形顶点的坐标,顶点按照逆时针顺序给出。
【输出】
输出文件名为polygon.out,共一行,包含一个非负整数,表示多边形内部的整点个数。
【输入输出样例】
|
polygon.in |
polygon.out |
|
7 0 3 1 1 4 2 7 1 5 3 8 5 2 6 |
20 |
【样例说明】
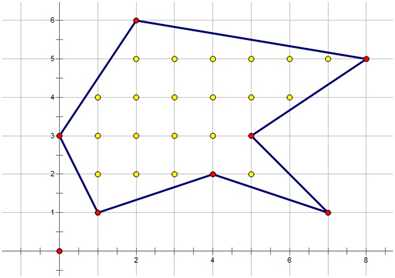
上图中黄色的点为多边形内部的整点,共20个。
考试题。。
计算几何第一题就来发一下吧。
首先搞pic定理:S=a+b/2-1(a是格点图形内的点数,b是边上的整点数)
所以只要求边上的整点,图形面积。
边上整点:(每条边的横竖坐标之差的绝对值的gcd)-1就是除这条边两个端点点上的所有点。
然后求面积。
叉积百度吧。。(math公式挂了没法解释了。。)
所以大约是以源点是一个节点,然后连n次,每次连输入中的1点和2点,2点和3点..n点和1点。
然后每次有两个向量.
它们的向量叉积之和就是面积和
至于证明自己推一下。。

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<cmath> 5 6 using namespace std; 7 8 #define maxn 100001 9 10 int gcd(int n,int m){return m==0?n:gcd(m,n%m);} 11 12 inline int in() 13 { 14 int x=0,f=1;char ch=getchar(); 15 while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘)ch=getchar(); 16 if(ch==‘-‘)f=-1,ch=getchar(); 17 while(ch>=‘0‘&&ch<=‘9‘)x=x*10+ch-‘0‘,ch=getchar(); 18 return x*f; 19 } 20 21 struct ed{ 22 int x,y; 23 }a[maxn+1]; 24 25 int main() 26 { 27 freopen("polygon.in","r",stdin); 28 freopen("polygon.out","w",stdout); 29 int n; 30 long long biandian=0,S=0; 31 n=in(); 32 for(int i=1;i<=n;i++) 33 a[i].x=in(),a[i].y=in(); 34 a[n+1]=a[1]; 35 for(int i=1;i<=n;i++) 36 { 37 biandian+=gcd(fabs(a[i+1].x-a[i].x),fabs(a[i+1].y-a[i].y)); 38 S+=(long long)a[i].x*a[i+1].y-(long long)a[i].y*a[i+1].x; 39 } 40 printf("%lld",(long long)(S+2-biandian)>>(long long)1); 41 return 0; 42 }

标签:
原文地址:http://www.cnblogs.com/tuigou/p/4875885.html