标签:
作者 白宁超
2015年10月13日23:23:13
摘要:程序员眼中的统计学系列是作者和团队共同学习笔记的整理。首先提到统计学,很多人认为是经济学或者数学的专利,与计算机并没有交集。诚然在传统学科中,其在以上学科发挥作用很大。然而随着科学技术的发展和机器智能的普及,统计学在机器智能中的作用越来越重要。本系列统计学的学习基于《深入浅出统计学》一书(偏向代码实现,需要读者有一定基础,可以参见后面PPT学习)。正如(吴军)先生在《数学之美》一书中阐述的,基于统计和数学模型对机器智能发挥重大的作用。诸如:语音识别、词性分析、机器翻译等世界级的难题也是从统计中找到开启成功之门钥匙的。尤其是在自然语言处理方面更显得重要,因此,对统计和数学建模的学习是尤为重要的。最后感谢团队所有人的参与。( 本文原创,转载注明出处:概率计算:把握机会 )
【程序员眼中的统计学(1)】 信息图形化:第一印象
【程序员眼中的统计学(2)】集中趋势度量:分散性、变异性、强大的距
【程序员眼中的统计学(3)】概率计算:把握机会
【程序员眼中的统计学(4)】离散概率分布的运用:善用期望
【程序员眼中的统计学(5)】排列组合:排序、排位、排
【程序员眼中的统计学(6)】几何分布、二项分布及泊松分布:坚持离散
【程序员眼中的统计学(7)】正态分布的运用:正态之美
【程序员眼中的统计学(8)】统计抽样的运用:抽取样本
【程序员眼中的统计学(9)】总体和样本的估计:进行预测
【程序员眼中的统计学(10)】假设检验的运用:研究证据
【程序员眼中的统计学(11)】卡方分布的应用
【程序员眼中的统计学(12)】相关与回归:我的线条如何?
我们将对自然现象的一次观察或进行一次科学试验称为试验。
举例1:硬币试验
E1: 抛一枚硬币,观察正(H)反(T) 面的情况。
E2: 将一枚硬币抛三次,观察正反面出现的情况。
E3: 将一枚硬币抛三次,观察出现正面的情况。
E4: 电话交换台一分钟内接到的呼唤次数。
E5: 在一批灯泡中任取一只, 测试它的寿命。
举例2:数学家去赌场
新闻:数学家3年赌赢156亿人民币,数学家在赌场里有什么优势?
令19名数学家惊喜的是,虽然他们所掌握的那些高深数学知识在现实生活中似乎派不上多大用场,但竟然出人意料地在赌场上显现出了巨大的威力!据悉,19名数学家参与的大多是赛马、赛狗以及21点之类的赌博项目。而每次下注之前,他们会利用自己所精通的专业数学方法对各种中奖的概率进行推理演算,从而研究出某种“逢赌必赢”的秘笈!因为它的形态看起来合乎理想。在现实生活中,遇到测量之类的大量连续数据时,你“正常情况下”会期望看到这种形态。
随机试验E的所有可能结果组成的集合称为 E的样本空间, 记为S。样本空间的元素称为样本点,用ω表示(有限个或可列个)。
离散样本空间: 样本点为有限个或可列个。例ω1, ω2等。
无穷样本空间: 样本点在区间或区域内取值。例:灯泡的寿命{t|t≥0}。
例如:只包含两个样本点的样本空间。
S={H,T} 其中ω1:H, ω2:T
以上既可以作为抛掷硬币出现正面或出现反面的模型, 也可以作为产品检验中合格与不合格的模型, 又能用于排队现象中有人排队与无人排队的模型等。



定义: 样本空间S的子集称为随机事件,简称事件。在一次试验中,当且仅当这一子集中的一个样本点出现时,称这一事件发生。
可能概型的两个特点:
(1)样本空间的元素只有有限个;
(2)实验中每个基本事件发生的可能性相同。
例如:掷一颗骰子,观察出现的点数。
概率的古典定义:
对于古典概型,样本空间S={w1, w2, … , wn},设事件A包含S的k个样本点,则事件A的概率定义为
(1) 选取适当的样本空间S, 使它满足有限等可能的要求, 且把事件A表示成S的某个子集.
(2) 计算样本点总数n及事件A包含的样本点数k.
(3) 用下列公式计算:


当随机试验的样本空间是某个区域,并且任意一点落在度量 (长度, 面积, 体积) 相同的子区域是等可能的,则事件 A 的概率可定义为:P(A)=m(A)/m(Ω)其中m(Ω)是样本空间的度量,m(A)是构成事件A的子区域的度量。借助于几何上的度量来合理规定的概率称为是几何概率。
说明: 当古典概型的试验结果为连续无穷多个时,就归结为几何概率。

(1) 对任一事件A ,有0≤p(A)≤1;
(2) p(Ω)=1,p(∅)=0;
(3) 对于两两互斥的可列多个事件A1,A2, ,P(A1 + A2 + ) = P(A1 )+P( A2 )
概率计算有时很复杂,因此,用图形方式表示概率往往十分有用。其中有一个办法是这样的:画一个方框代表样本空间S,然后画几个圆圈代表各个相关事件,这种图称为维恩图。如下图所示:
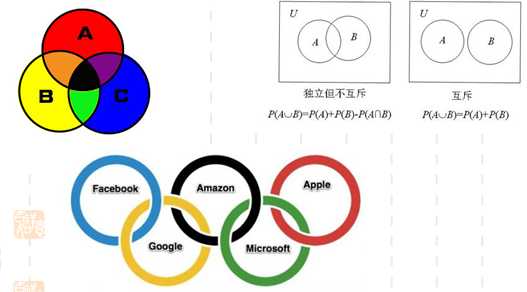
优点: 在用图形方式表现概率问题时,维恩图会是一个很有用的工具,同时在集合的划分上也会有很大的帮助。
不足: 不方便表现条件概率。
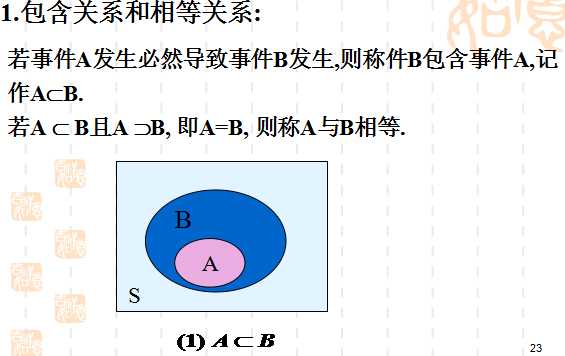
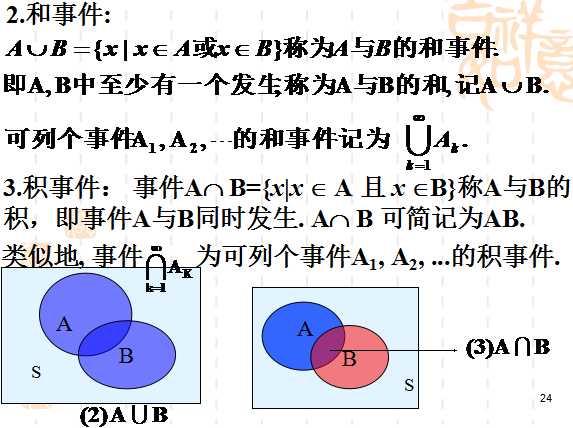
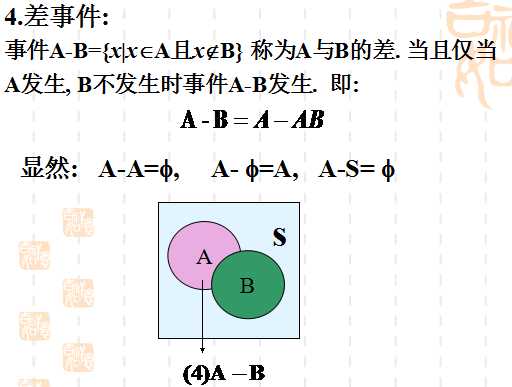
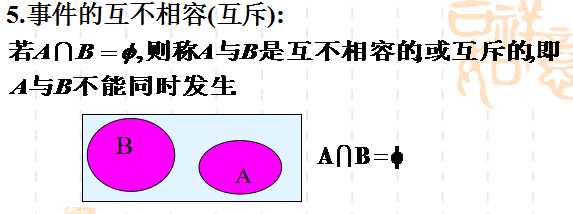
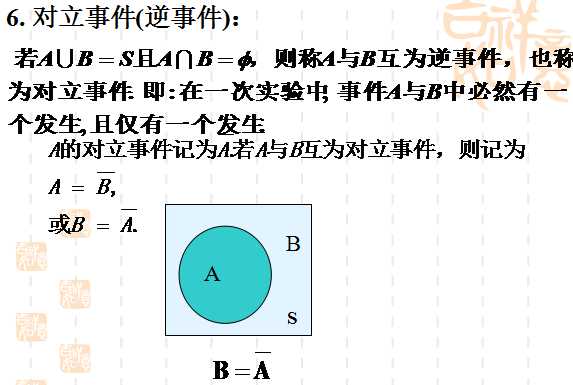
设S是样本空间, E是随机试验. 对于E的每个事件A对应一个实数P(A), 称为事件 A的概率, 其中集合函数P(.)满足下列条件:
(1) 对任一事件A,有P(A)≥0; (非负性)
(2) P(S)=1;(规范性)
(3) 设A1,A2,…是两两互不相容的事件,则有P(A1A2…)=P(A1)+P(A2)+… (可列可加性)
性质1. p(Φ)=0
性质2. 若A1,A2.··· · · An是两两互不相容的事件,则P(A1UA2U....UAn)=P(A1)+P(A2)+.....+P(An)(可列可加性)
性质3. 若A包含于B,则有P(B-A)=P(B)-P(A);P(B)>=P(A)
性质4. 对于任意一个事件A, P(A)<=1
性质5. 对任一事件A, p(A‘)=1-P(A)
性质6. 对于任意两事件A,B,有: P(AUB)=P(A)+P(B)-P(AB)
设试验E的样本空间为S, A, B是事件, 要考虑在A已经发生的条件下B发生的概率, 这就是条件概率问题。
设A,B是两个事件,且P(A)>0,称: P(A|B)=P(AB)/P(A)
性质1. 对于每一个事件B,有: 1>=P(B|A)>=0
性质2. P(S|A)=1
性质3. 设B1,B2· · ·两两互不相容,则 P(UBi|A)=∑P(Bi|A)
(1)公式法:
先计算P(A),P(AB),然后按公式计算P(B|A)=P(AB)/P(A)
(2)图解法:利用概率树求解
案例一:
图圈饼店正在调查客户购买圈饼和咖啡的概率,下面是一些线索,画出概率树并求解相应概率。以下是已知条件:
P(圈饼) = 3/4
P(咖啡|圈饼’) = 1/3
P(圈饼∩咖啡) = 9/20
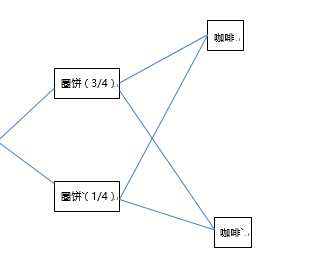
计算过程:
P(咖啡|圈饼) = P(圈饼∩咖啡) / P(圈饼) = 3/5;
P(咖啡|圈饼`) = P(圈饼`∩咖啡) / P(圈饼`) = 1/3;
P(咖啡`|圈饼) = P(圈饼∩咖啡`) / P(圈饼) = 2/5;
P(咖啡`|圈饼`) = P(圈饼`∩咖啡`) / P(圈饼`) = 2/3;
(1)优点: 能够以图形体现条件概率,同时帮助计算概率,利用分支结构,条理清楚,不易算错。
(2)不足: 画概率树很浪费时间。
/** * 计算条件概率 * * @param pOfA 概率P(A) * @param pOfAB 概率P(AB) * @return 概率P(B|A) */ public static float CondProFunc(float pOfA, float pOfAB){ String temp; BufferedReader brd=new BufferedReader(new InputStreamReader(System.in)); while(true){ //请用户输入概率P(A)的值 System.out.print("Input the number of pOfA(输入非零正整数):\n") ; try{ temp=brd.readLine() ; pOfA=Float.parseFloat(temp) ;//概率P(A) //概率P(A)不能为0,不能是负数; if (pOfA <= 0) { System.out.println("输入类型错误!已退出!") ; return 0; } break; }catch(Exception e){ System.out.println("对不起,只能输入非零数,请重新输入。") ; } } System.out.println("你输入的pOfA是: "+ pOfA) ; while(true){ //请用户输入概率P(AB)的值 System.out.print("Input the number of pOfAB:\n") ; try{ temp=brd.readLine() ; pOfAB=Float.parseFloat(temp) ;//概率P(AB) break; }catch(Exception e){ System.out.println("对不起,只能输入非零数,请重新输入。") ; } } System.out.println("你输入的pOfAB是: "+ pOfAB) ; return pOfAB/pOfA; }
设B1 ,B2 , ··· · · Bn 为S的一个划分,P(Bi)>0,(i = 1,2 · · ·,n),A为E的事件,则P(A) =∑P(Bi)P(A|Bi) ,称为全概率公式。
/** * 计算全概率 * @param Bi 概率P(Bi); * @param A_Bi 条件概率P(A|Bi); * @return 返回全概率P(A); */ static float TotalProb(int num, float[] Bi, float[] A_Bi) { float pA = 0;//全概率P(A) for (int i = 0; i < num; i++) { pA += A_Bi[i] * Bi[i]; } return pA; }
设B1 ,B2 , ··· · · Bn 为S的一个划分,P(Bi)>0,(i = 1,2 · · ·,n),A是一个随机事件,且P(A)>0,则有
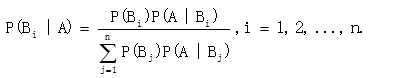
称为贝叶斯公式。
/** * 计算贝叶斯概率 * @param Bi 概率P(Bi); * @param A_Bi 条件概率P(A|Bi); * @return 返回贝叶斯概率P(Bi|A); */ static float[] BayesProb(int num, float[] Bi, float[] A_Bi) { float pA = 0;//全概率P(A) Bi_A = new float[num];//概率P(Bi|A) for (int i = 0; i < num; i++) { pA += A_Bi[i] * Bi[i]; } for (int i = 0; i < num; i++) { Bi_A[i] = (A_Bi[i]*Bi[i])/pA ; } return Bi_A; }
全概公式:首先需要建立一个完备事件组,实际上全概率就是已知第一阶段,然后再求第二阶段,比如第一阶段分A B C三种,然后A B C中均有D发生的概率,最后求D的概率P(D)=P(A)*P(D/A)+P(B)*P(D/B)+P(C)*P(D/C)
贝叶斯公式:贝叶斯其实就是已知第二阶段,然后去反推第一阶段的求后验概率,这时候关键是利用条件概率公式做转换。此时全概率作为分母。P(A/D)=P(AD)/P(D)=P(A)*P(D/A)/P(D)
案例:
食用奶粉发生中毒事件,已知有三种品牌的奶粉,分别为:A. 三鹿 B. 伊利 C. 光明
问题一:已知在三种奶粉存在情况下,患病的概率。
问题二:已知在患病的前提下,求由于三鹿奶粉导致患病的概率。
解答:
1.全概公式: P(D)=P(A)*P(D/A)+P(B)*P(D/B)+P(C)*P(D/C)
2.贝叶斯公式:P(A/D)=P(AD)/P(D)=P(A)*P(D/A)/P(D)
设A,B是试验E的两事件,当P(A)>0, 可以定义P(B|A)=P(AB)/P(A)
一般地, P(B|A)≠P(B), 但当A的发生对B的发生的概率没有影响时,有P(B|A)=P(B),由乘法公式有P(AB)=P(A)P(B|A)=P(A)P(B).
设试验E为掷甲、乙两枚硬币,观察正反面出现情况. 设A—“甲币出现H”, B—“乙币出现H”, 试求:B发生的条件下,A发生的概率
由定义可知:
1) 零概率事件与任何事件都是相互独立的。
2) 由对称性, A,B相互独立, 必有B, A 相互独立。
设A,B是两事件,且P(A)>0,则A,B相互独立的充要条件是: P(B|A)=P(B).
有如下结论:
(1) 若A,B相互独立,则 A与B‘,A‘与B,A‘与B‘也相互独立。
(2)P(A)>0,P(B)>0, 则A,B相互独立与A,B互斥不能同时成立。
样本空间: 我们将随机实验E的一切可能基本结果组成的集合称为E的样本空间,记为S。样本空间的元素,即E的每一个可能的结果,称为样本点。样本空间又叫基本事件空间。
随机事件具有的特点如下:
a.可以在相同的条件下重复进行;
b.每个试验的可能结果不止一个,并且能事先预测试验的所有可能结果;
c.进行一次试验之前不能确定哪一个结果会出现。
概率的性质:
性质1. P(Φ)=0.
性质2. (有限可加性)当n个事件A1,…,An两两互不相容时: P(A1∪...∪An)=P(A1)+...+P(An).
性质3. 对于任意一个事件A:P(A)=1-P(非A).
性质4. 当事件A,B满足A包含于B时:P(B-A)=P(B)-P(A),P(A)≤P(B).
性质5. 对于任意一个事件A,P(A)≤1.
性质6. 对任意两个事件A和B,P(B-A)=P(B)-P(AB).
性质7. (加法公式)对任意两个事件A和B,P(A∪B)=P(A)+P(B)-P(A∩B)
维恩图: 维恩图的适用场景是帮助我们做些简单概率的计算,比如交集,并集,补集。但是过于复杂的概率计算,比如条件概率,并不适合用维恩图来表示,这时,概率树可以帮助我们计算条件概率。
全概率公式: 首先建立一个完备事件组,然后一定是在已知第一阶段的基础上,求第二阶段事件发生的概率。
贝叶斯公式:贝叶斯其实就是已知第二阶段,然后去反推第一阶段的求后验概率,这时候关键是利用条件概率公式做转换。此时全概率作为分母。
事件的独立性:最简单就是利用P(AB)=P(A)P(B)来判断,因为这一公式与事件独立是充要条件,在实际应用中简单方便。
特别要注意的是,A与B相互独立,A与B互斥是不能同时成立的。
全概率公式与贝叶斯公式的区别:在具体应用上结合题目要求,选择恰当的公式求解,可以记住特例来判断。
互斥事件与独立事件的区别:互斥事件就是彼此相互制约,此发生彼就不能发生;独立事件就是彼此发生与否没有关系。

标签:
原文地址:http://www.cnblogs.com/baiboy/p/tjx3.html