标签:
Lattice paths
Problem_15
Starting in the top left corner of a 2×2 grid,and only being able to move to the right and down,there are exactly 6 routes to the bottom right corner.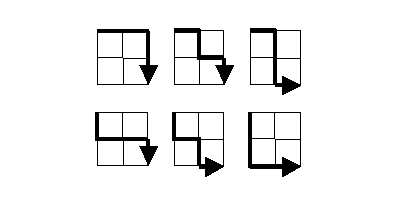
How many such routes are there through a 20*20 grid?
从一个2×2网格的左上角开始,有6条(最短)通往右下角的路。对于20×20的网格,这样的路有多少条?
注:题目链接:https://projecteuler.net/problem=15
试想一下2×2的方格中从左上角到右下角一共需要4步,假如向下的两步确定了,那么向右的两步是不是也就确定了。
再比如有20个板凳,10男10女,当男生都坐下来的时候,女生的位置也就确定了,那么一共有多少种情况!Combination(20,10)种情况!
这题也是如此,一共需要走40步,当向下的步都确定时。向右的步也都跟着确定了。所以这一题的答案便是Combination(40,20)!
接下来只需要求组合数C(40,20)就可以了!或者也可以通过遍历求出一种有多少条?
前些日子,因为要做概率论与数理统计的作业,有些题目需要计算C(m,n),题目一多,自己约分也挺麻烦,就萌生了自己写个代码求约分后的每一项!
1 #include<iostream> 2 using namespace std; 3 4 int GCD(int num_m,int num_n) 5 { 6 int tmp; 7 if(num_m<num_n) 8 { 9 tmp=num_m; 10 num_m=num_n; 11 num_n=tmp; 12 } 13 while(tmp=num_m%num_n) 14 { 15 num_m=num_n; 16 num_n=tmp; 17 } 18 return num_n; 19 } 20 21 void Combination(int m,int n) 22 { 23 if(m==n) 24 { 25 cout<<1<<endl; 26 } 27 28 int M[n]; 29 int N[n]; 30 int i; 31 for(i=0;i<n;i++) 32 { 33 M[i]=m-i; 34 N[i]=n-i; 35 } 36 int tmp=n; 37 int j=0,k=0; 38 int GCD_return; 39 int temp; 40 while(n>1) 41 { 42 if(M[j]%N[k]==0&&N[k]!=1) 43 { 44 M[j]=M[j]/N[k]; 45 for(temp=k;temp<n-2;temp++) 46 { 47 N[temp]=N[temp+1]; 48 } 49 n--; 50 if(k==n-1) 51 { 52 k=0; 53 } 54 } 55 else 56 { 57 GCD_return=GCD(M[j],N[k]); 58 if(GCD_return>1) 59 { 60 M[j]=M[j]/GCD_return; 61 N[k]=N[k]/GCD_return; 62 } 63 if(k==n-1) 64 { 65 k=0; 66 j++; 67 } 68 else 69 { 70 k++; 71 } 72 } 73 } 74 for(i=0;i<tmp;i++) 75 { 76 if(M[i]!=1) 77 cout<<M[i]<<‘,‘; 78 } 79 cout<<endl; 80 } 81 82 int main() 83 { 84 Combination(10,5); 85 Combination(40,20); 86 Combination(4,1); 87 Combination(12,8); 88 Combination(8,8); 89 return 0; 90 }
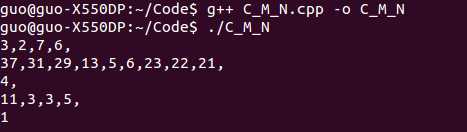
而C(40,20)=37×31×29×13×5×6×23×22×21=137846528820也就是该题的答案
数据测试的不多,并不能保证代码的正确性。
通过学到的去解决一些小问题!
标签:
原文地址:http://www.cnblogs.com/Guth/p/4878386.html