最近博主的老师让博主写一个二分查找,并且计算他的时间复杂度。
首先我是这样写的:
1 #include<stdio.h>
2 #include<assert.h>
3
4 void binary_search(int arr[],int len,int num){
5 assert(arr);
6 int left = 0;
7 int right = len-1;
8 while(left<right){
9 int mid = (left+right)/2;
10 if(num == arr[mid]){
11 printf("%d\n",mid);
12 break;
13 }
14 else if(num > arr[mid])
15 left = mid+1;
16 else if(num < arr[mid])
17 right = mid-1;
18 else
19 printf("not find\n");
20 }
21 }
22
23 int main(){
24 int arr[] = {1,2,3,4,5,6,7,8};
25 int len = sizeof(arr)/sizeof(arr[0]);
26 int num = 7;
27 binary_search(arr,len,num);
28 return 0;
29 }
但是这里有两个明显的bug:
1. while(left<right)里边界判断条件应该写成while(left<=right),试想当数组只有一个元素时就会出现错误结果;
2. int mid = (left+right)/2;也有问题,当 left+right的值相当大超出了int型整数的范围时,就会溢出。应该写成 int mid = left+(right-left)/2 。
接下来我们来看看二分查找的时间复杂度为什么是O(logn)
关于二分查找的思想:首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
关于满二叉树:一棵深度为h且有 2^h-1个结点的二叉树。满二叉树是一种特殊的完全二叉树。表示为:
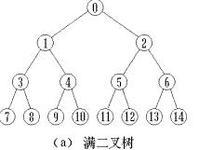
假设现在有一棵满二叉树,他的左孩子都小于根节点,右孩子都大于根节点,然后我们发现二分查找(升序)其实就是满排序二叉树!!那么现在我们将根节点看作每次查找的arr[mid],要找到某一个元素需要将这一棵树展开,我们记作2^h-1=n,也就是说展开的次数h=log2^(n+1).
这里的h就是查找所需的次数,用O的渐进表示法就是O(log2^n).
楼主表达能力有限,各位有没有细思极恐嘞?
本文出自 “moLova” 博客,请务必保留此出处http://molova.blog.51cto.com/10594266/1703764
原文地址:http://molova.blog.51cto.com/10594266/1703764