标签:
图主要有深度优先遍历(DFS)和广度优先遍历(BFS)。
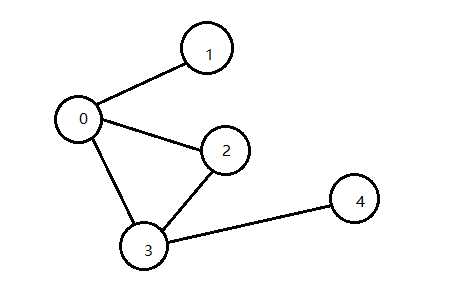
深度优先类似于树的先序遍历,从要访问的节点(0)出发,选取和它相邻的任何一个节点(3),访问之,再访问和3相邻的节点(4),访问之,直到访问到没有相邻节点的节点,比如4没有相邻节点了,那么就回溯一层,访问3的未被访问的邻接节点。如图所示。直到所有的顶点均被访问。
所以深度优先就需要我们递归地检查每个顶点。
所用的图的存储结构是上一篇中讲的邻接表存储。
void DFS(AGraph *g,int v) { Edge *p; visit[v]=1; printf("%d\n",v); p=g->adjlist[v].firstEdge; while(p!=NULL) { if(visit[p->adjvex]==0) DFS(g,p->adjvex); p=p->nextEdge; } }
visit数组记录当前是否被访问。
广度优先遍历类似于树的层次遍历。以上图为例,首先访问节点0,访问和0邻接的所有节点(1、2、3),然后访问节点(1、2、3)的全部邻接节点,直到所有的节点被访问。
所以,BFS就需要用到队列,初始时,将初始节点入队,访问队首节点,将所有和它邻接且未被访问过的节点访问并入队,顶点出队,循环上述操作,直到所有节点访问一遍(即队空)。
总结就是——访问、所有邻接节点访问入队,出队,访问所有邻接节点入队……直到队空
1 void BFS(AGraph *g,int v,int n) 2 { 3 Edge *p; 4 int que[MAXSIZE]; 5 int fro=0; //队首 6 int rea=0; //队尾 7 printf("%d\n",v); 8 visit[v]=1; 9 rea = (rea+1)%n; 10 que[rea]=v; 11 int j; 12 while(fro!=rea) 13 { 14 fro=(fro+1)%n; 15 j=que[fro]; 16 p=g->adjlist[j].firstEdge; 17 while(p!=NULL) 18 { 19 if(visit[p->adjvex]==0) 20 { 21 printf("%d\n",p->adjvex); 22 visit[p->adjvex]=1; 23 rea=(rea+1)%n; 24 que[rea]=p->adjvex; 25 } 26 p=p->nextEdge; 27 } 28 } 29 }
标签:
原文地址:http://www.cnblogs.com/wktwj/p/4892297.html