线性回归练习

时间：2015-10-19 17:42:57 阅读：340 评论：0 收藏：0 [点我收藏+]

标签：

首先下载训练集数据ex2Data.zip, 里面有50个训练样本，x为50位小朋友的年龄，年龄段为2岁至8岁，y为对应小朋友的身高，年龄和身高都可以表示为小数形式，现在的需求是根据这50位小朋友的样本数据预测3.5岁和7岁小朋友的身高。

下面，我们首先画出这50位小朋友样本数据的散点图，使用的工具为Matlab。

第一步：加载数据

    x = load(‘ex2x.dat‘);
    y = load(‘ex2y.dat‘);

第二步：画散点图

figure %open a new figure window
plot(x, y, ‘o‘);
ylabel(‘Height in meters‘)
xlabel(‘Age in years‘)

技术分享

通过上图，我们可以直观的发现，这些数据可以利用线性回归模型处理。我们在这里分别利用正规方程组和梯度下降两种方式求解。

方法一：正规方程求解

在线性规划、梯度下降、正规方程组——斯坦福ML公开课笔记1-2中，我们曾经讲过关于正规方程组求解的方法。最后求解得到：

技术分享

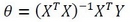
Matlab实现如下：

%%方法一
x = load(‘ex2x.dat‘); %加载数据
y = load(‘ex2y.dat‘);
plot(x,y,‘o‘)         %画散点图
xlabel(‘height‘)      %横轴含义标签
ylabel(‘age‘)
x = [ones(length(x),1),x];   
% ones(length(x),1)用1填充x第一列长度的列向量（50*1）
% x = [ones(length(x),1),x]是在原来x基础上添加了一列全为1的列向量(50*2)
w=inv(x‘*x)*x‘*y   % 这个就是我们正规方程组求解公式，inv()是求逆，X‘是X转置
hold on            %仍在上面散点图画布上画图
plot(x(:,2),0.0639*x(:,2)+0.7502)  %w=inv(x‘*x)*x‘*y求解得到w0和w1
% w0=0.7502,w1=0.0639,所以直线方程为0.0639*x(:,2)+0.7502，其中x(:,2)代表x中第二列数据，即原始训练数据集中的年龄数据

方法二：梯度下降法

我们需要设定迭代次数（1500次）和学习率（alpha=0.07），并根据上面个两个式子迭代计算梯度求解。具体编程实现如下：

clear all; close all; clc

x = load(‘ex2x.dat‘); 
y = load(‘ex2y.dat‘);

m = length(y); % number of training examples

% Plot the training data
figure; % open a new figure window
plot(x, y, ‘o‘);
ylabel(‘Height‘)
xlabel(‘Age‘)

% Gradient descent
x = [ones(m, 1) x]; % Add a column of ones to x
theta = zeros(size(x(1,:)))‘; % initialize fitting parameters
% 用零填充x第一行数据大小的向量（1*2），再转置为列向量（2*1）
MAX_ITR = 1500; % 最大迭代次数
alpha = 0.07;   % 学习率的大小

for num_iterations = 1:MAX_ITR   
    % Here is the gradient
    grad = (1/m).* x‘ * ((x * theta) - y);   
    % Here is the actual update
    theta = theta - alpha .* grad;
end

% print theta to screen
theta

% Plot the linear fit
hold on; % keep previous plot visible
plot(x(:,2), x*theta, ‘-‘)
legend(‘Training data‘, ‘Linear regression‘)%标出图像中各曲线标志所代表的意义，图例的意思
hold off % don‘t overlay any more plots on this figure，指关掉前面的那幅图

% Closed form solution for reference
% You will learn about this method in future videos
exact_theta = (x‘ * x)\x‘ * y

% Predict values for age 3.5 and 7
predict1 = [1, 3.5] *theta
predict2 = [1, 7] * theta


% Calculate J matrix损失函数
% Grid over which we will calculate J
theta0_vals = linspace(-3, 3, 100);%在-3到3的区间中均匀生成100个值
theta1_vals = linspace(-1, 1, 100);

% initialize J_vals to a matrix of 0‘s
J_vals = zeros(length(theta0_vals), length(theta1_vals));

for i = 1:length(theta0_vals)
      for j = 1:length(theta1_vals)
      t = [theta0_vals(i); theta1_vals(j)];    
      J_vals(i,j) = (0.5/m) .* (x * t - y)‘ * (x * t - y);
    end
end

% Because of the way meshgrids work in the surf command, we need to 
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals‘;
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel(‘\theta_0‘); ylabel(‘\theta_1‘);

% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 2, 15))%画出等高线
xlabel(‘\theta_0‘); ylabel(‘\theta_1‘);%类似于转义字符，但是最多只能是到参数0~9

技术分享