最小二乘法的推导证明

标签：

1、附加题：推导线性最小二乘法过程

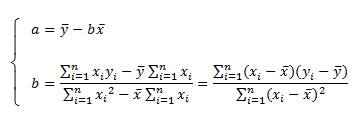
上述式子求解b 时最后一步用到求和性质，事实上

同理可证分子部分，具体请参考《计量经济学导论（第四版）Introductory Econometrics A Modern Approach Fourth Edition · 杰弗里·M·伍德里奇（Jeffrey M. Wooldridge）著》中的附录A 基本数学工具 。

2、赛马问题

问：36匹马，6条跑道，无计时器，最少几次比赛可以选出前3名？

答案是8次，思路如下：

（1）把36匹马分成6组，分别进行6次比赛，可以得出每一组的第1名。

（2）把每组的第1名再进行1次比赛，分别得到各组最快的马匹的排名。

（3）选取第1名所在的组的第1、2、3名，第2名所在的组的第1、2名（第3名不用选取，因为他最好的成绩也就是第4名），第3名所在的组的第1名（同上推理），第4、5、6名所在的组不用再进行比赛（同上推理），组成6个人再进行1次比赛，即可得出前3名。

综上所述，总共6+1+1=8次比赛。

3、随机数

现有一个rand5()的随机数生成器，等可能地生成1~5之间的数，要求用它实现rand7()，等可能地生成1~7之间的数。

思路：把1-5映射到7的倍数空间，例如调用2次rand5()相乘可以得到1~25的空间，每个数都是等可能地1/25，再写一个判断函数扔掉22-25，留下1~21。

提示：“等可能”只是说每个数产生的概率相等，并不意味着加起来等于1。

def rand7():
    r = 25
    while(r>21):
        a = rand5()
        b = rand5()
        r = a * b
    return r / 3

最小二乘法的推导证明

标签：

原文地址：http://my.oschina.net/keyven/blog/519571