uva 11275 3D Triangles

时间：2015-10-22 00:16:00 阅读：292 评论：0 收藏：0 [点我收藏+]

标签：

题意：三维空间中，给出两个三角形的左边，问是否相交。

面积法判断点在三角形内：

  1 #include<cstdio>
  2 #include<cmath>
  3 #include<cstring>
  4 #include<algorithm>
  5 #include<iostream>
  6 #include<memory.h>
  7 #include<cstdlib>
  8 #include<vector>
  9 #define clc(a,b) memset(a,b,sizeof(a))
 10 #define LL long long int
 11 #define up(i,x,y) for(i=x;i<=y;i++)
 12 #define w(a) while(a)
 13 const double inf=0x3f3f3f3f;
 14 const double PI = acos(-1.0);
 15 using namespace std;
 16 
 17 struct Point3
 18 {
 19     double x, y, z;
 20     Point3(double x=0, double y=0, double z=0):x(x),y(y),z(z) { }
 21 };
 22 
 23 typedef Point3 Vector3;
 24 
 25 Vector3 operator + (const Vector3& A, const Vector3& B)
 26 {
 27     return Vector3(A.x+B.x, A.y+B.y, A.z+B.z);
 28 }
 29 Vector3 operator - (const Point3& A, const Point3& B)
 30 {
 31     return Vector3(A.x-B.x, A.y-B.y, A.z-B.z);
 32 }
 33 Vector3 operator * (const Vector3& A, double p)
 34 {
 35     return Vector3(A.x*p, A.y*p, A.z*p);
 36 }
 37 Vector3 operator / (const Vector3& A, double p)
 38 {
 39     return Vector3(A.x/p, A.y/p, A.z/p);
 40 }
 41 
 42 const double eps = 1e-8;
 43 int dcmp(double x)
 44 {
 45     if(fabs(x) < eps) return 0;
 46     else return x < 0 ? -1 : 1;
 47 }
 48 
 49 double Dot(const Vector3& A, const Vector3& B)
 50 {
 51     return A.x*B.x + A.y*B.y + A.z*B.z;
 52 }
 53 double Length(const Vector3& A)
 54 {
 55     return sqrt(Dot(A, A));
 56 }
 57 double Angle(const Vector3& A, const Vector3& B)
 58 {
 59     return acos(Dot(A, B) / Length(A) / Length(B));
 60 }
 61 Vector3 Cross(const Vector3& A, const Vector3& B)
 62 {
 63     return Vector3(A.y*B.z - A.z*B.y, A.z*B.x - A.x*B.z, A.x*B.y - A.y*B.x);
 64 }
 65 double Area2(const Point3& A, const Point3& B, const Point3& C)
 66 {
 67     return Length(Cross(B-A, C-A));
 68 }
 69 
 70 Point3 read_point3()
 71 {
 72     Point3 p;
 73     scanf("%lf%lf%lf", &p.x, &p.y, &p.z);
 74     return p;
 75 }
 76 
 77 // 点在三角形P0, P1, P2中
 78 bool PointInTri(const Point3& P, const Point3& P0, const Point3& P1, const Point3& P2)
 79 {
 80     double area1 = Area2(P, P0, P1);
 81     double area2 = Area2(P, P1, P2);
 82     double area3 = Area2(P, P2, P0);
 83     return dcmp(area1 + area2 + area3 - Area2(P0, P1, P2)) == 0;
 84 }
 85 
 86 // 三角形P0P1P2是否和线段AB相交
 87 bool TriSegIntersection(const Point3& P0, const Point3& P1, const Point3& P2, const Point3& A, const Point3& B, Point3& P)
 88 {
 89     Vector3 n = Cross(P1-P0, P2-P0);
 90     if(dcmp(Dot(n, B-A)) == 0) return false; // 线段A-B和平面P0P1P2平行或共面
 91     else   // 平面A和直线P1-P2有惟一交点
 92     {
 93         double t = Dot(n, P0-A) / Dot(n, B-A);
 94         if(dcmp(t) < 0 || dcmp(t-1) > 0) return false; // 不在线段AB上
 95         P = A + (B-A)*t; // 交点
 96         return PointInTri(P, P0, P1, P2);
 97     }
 98 }
 99 
100 bool TriTriIntersection(Point3* T1, Point3* T2)
101 {
102     Point3 P;
103     for(int i = 0; i < 3; i++)
104     {
105         if(TriSegIntersection(T1[0], T1[1], T1[2], T2[i], T2[(i+1)%3], P)) return true;
106         if(TriSegIntersection(T2[0], T2[1], T2[2], T1[i], T1[(i+1)%3], P)) return true;
107     }
108     return false;
109 }
110 
111 int main()
112 {
113     int T;
114     scanf("%d", &T);
115     while(T--)
116     {
117         Point3 T1[3], T2[3];
118         for(int i = 0; i < 3; i++) T1[i] = read_point3();
119         for(int i = 0; i < 3; i++) T2[i] = read_point3();
120         printf("%d\n", TriTriIntersection(T1, T2) ? 1 : 0);
121     }
122     return 0;
123 }

View Code

用Barycentric坐标法判断点在三角形内（重心法）

  1 #include<cstdio>
  2 #include<cmath>
  3 using namespace std;
  4 
  5 struct Point3
  6 {
  7     double x, y, z;
  8     Point3(double x=0, double y=0, double z=0):x(x),y(y),z(z) { }
  9 };
 10 
 11 typedef Point3 Vector3;
 12 
 13 Vector3 operator + (const Vector3& A, const Vector3& B)
 14 {
 15     return Vector3(A.x+B.x, A.y+B.y, A.z+B.z);
 16 }
 17 Vector3 operator - (const Point3& A, const Point3& B)
 18 {
 19     return Vector3(A.x-B.x, A.y-B.y, A.z-B.z);
 20 }
 21 Vector3 operator * (const Vector3& A, double p)
 22 {
 23     return Vector3(A.x*p, A.y*p, A.z*p);
 24 }
 25 Vector3 operator / (const Vector3& A, double p)
 26 {
 27     return Vector3(A.x/p, A.y/p, A.z/p);
 28 }
 29 
 30 const double eps = 1e-8;
 31 int dcmp(double x)
 32 {
 33     if(fabs(x) < eps) return 0;
 34     else return x < 0 ? -1 : 1;
 35 }
 36 
 37 double Dot(const Vector3& A, const Vector3& B)
 38 {
 39     return A.x*B.x + A.y*B.y + A.z*B.z;
 40 }
 41 double Length(const Vector3& A)
 42 {
 43     return sqrt(Dot(A, A));
 44 }
 45 double Angle(const Vector3& A, const Vector3& B)
 46 {
 47     return acos(Dot(A, B) / Length(A) / Length(B));
 48 }
 49 Vector3 Cross(const Vector3& A, const Vector3& B)
 50 {
 51     return Vector3(A.y*B.z - A.z*B.y, A.z*B.x - A.x*B.z, A.x*B.y - A.y*B.x);
 52 }
 53 double Area2(const Point3& A, const Point3& B, const Point3& C)
 54 {
 55     return Length(Cross(B-A, C-A));
 56 }
 57 
 58 Point3 read_point3()
 59 {
 60     Point3 p;
 61     scanf("%lf%lf%lf", &p.x, &p.y, &p.z);
 62     return p;
 63 }
 64 
 65 // 点在三角形P0, P1, P2中
 66 // http://www.blackpawn.com/texts/pointinpoly/default.html
 67 bool PointInTri(const Point3& P, const Point3& P0, const Point3& P1, const Point3& P2)
 68 {
 69     Vector3 v0 = P2 - P0;
 70     Vector3 v1 = P1 - P0;
 71     Vector3 v2 = P - P0;
 72 
 73     // Compute dot products
 74     double dot00 = Dot(v0, v0);
 75     double dot01 = Dot(v0, v1);
 76     double dot02 = Dot(v0, v2);
 77     double dot11 = Dot(v1, v1);
 78     double dot12 = Dot(v1, v2);
 79 
 80     // Compute barycentric coordinates
 81     double invDenom = 1 / (dot00 * dot11 - dot01 * dot01);
 82     double u = (dot11 * dot02 - dot01 * dot12) * invDenom;
 83     double v = (dot00 * dot12 - dot01 * dot02) * invDenom;
 84 
 85     // Check if point is in triangle
 86     return (dcmp(u) >= 0) && (dcmp(v) >= 0) && (dcmp(u + v - 1) <= 0);
 87 }
 88 
 89 // 三角形P0P1P2是否和线段AB相交
 90 bool TriSegIntersection(const Point3& P0, const Point3& P1, const Point3& P2, const Point3& A, const Point3& B, Point3& P)
 91 {
 92     Vector3 n = Cross(P1-P0, P2-P0);
 93     if(dcmp(Dot(n, B-A)) == 0) return false; // 线段A-B和平面P0P1P2平行或共面
 94     else   // 平面A和直线P1-P2有惟一交点
 95     {
 96         double t = Dot(n, P0-A) / Dot(n, B-A);
 97         if(dcmp(t) < 0 || dcmp(t-1) > 0) return false; // 不在线段AB上
 98         P = A + (B-A)*t; // 交点
 99         return PointInTri(P, P0, P1, P2);
100     }
101 }
102 
103 bool TriTriIntersection(Point3* T1, Point3* T2)
104 {
105     Point3 P;
106     for(int i = 0; i < 3; i++)
107     {
108         if(TriSegIntersection(T1[0], T1[1], T1[2], T2[i], T2[(i+1)%3], P)) return true;
109         if(TriSegIntersection(T2[0], T2[1], T2[2], T1[i], T1[(i+1)%3], P)) return true;
110     }
111     return false;
112 }
113 
114 int main()
115 {
116     int T;
117     scanf("%d", &T);
118     while(T--)
119     {
120         Point3 T1[3], T2[3];
121         for(int i = 0; i < 3; i++) T1[i] = read_point3();
122         for(int i = 0; i < 3; i++) T2[i] = read_point3();
123         printf("%d\n", TriTriIntersection(T1, T2) ? 1 : 0);
124     }
125     return 0;
126 }

View Code

证明可以参考http://www.cnblogs.com/graphics/archive/2010/08/05/1793393.html

三角形的三个点在同一个平面上，如果选中其中一个点，其他两个点不过是相对该点的位移而已，比如选择点A作为起点，那么点B相当于在AB方向移动一段距离得到，而点C相当于在AC方向移动一段距离得到。

技术分享

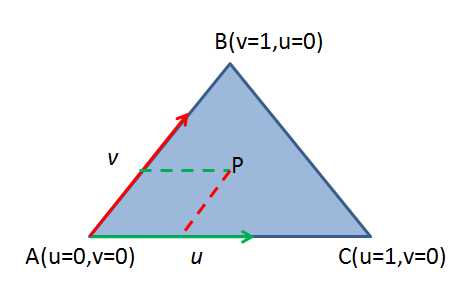
所以对于平面内任意一点，都可以由如下方程来表示

P = A + u * (C – A) + v * (B - A) // 方程1

如果系数u或v为负值，那么相当于朝相反的方向移动，即BA或CA方向。那么如果想让P位于三角形ABC内部，u和v必须满足什么条件呢？有如下三个条件

u >= 0

v >= 0

u + v <= 1

几个边界情况，当u = 0且v = 0时，就是点A，当u = 0,v = 1时，就是点B，而当u = 1, v = 0时，就是点C

整理方程1得到P – A = u(C - A) + v(B - A)

令v0 = C – A, v1 = B – A, v2 = P – A，则v2 = u * v0 + v * v1，现在是一个方程，两个未知数，无法解出u和v，将等式两边分别点乘v0和v1的到两个等式

(v2) • v0 = (u * v0 + v * v1) • v0

(v2) • v1 = (u * v0 + v * v1) • v1

注意到这里u和v是数，而v0，v1和v2是向量，所以可以将点积展开得到下面的式子。

v2 • v0 = u * (v0 • v0) + v * (v1 • v0) // 式1

v2 • v1 = u * (v0 • v1) + v * (v1• v1) // 式2

解这个方程得到

u = ((v1•v1)(v2•v0)-(v1•v0)(v2•v1)) / ((v0•v0)(v1•v1) - (v0•v1)(v1•v0))

v = ((v0•v0)(v2•v1)-(v0•v1)(v2•v0)) / ((v0•v0)(v1•v1) - (v0•v1)(v1•v0))

uva 11275 3D Triangles

标签：

原文地址：http://www.cnblogs.com/ITUPC/p/4899607.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行