[POJ 1390]Blocks

标签：dp   记忆化dfs   

Description

Some of you may have played a game called ‘Blocks‘. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold.
The corresponding picture will be as shown below:

Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a ‘box segment‘. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.

Now let‘s look at the picture below:

Figure 2

The first one is OPTIMAL.

Find the highest score you can get, given an initial state of this game.

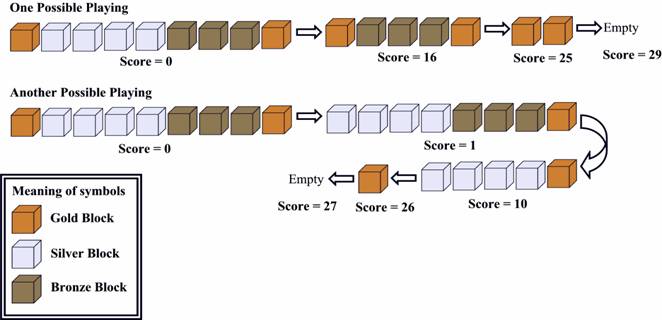
Input

Output

Sample Input

2
9
1 2 2 2 2 3 3 3 1
1
1

Sample Output

Case 1: 29
Case 2: 1

Source

LRJ出的题果然诡异！这个DP很奇怪，因为状态很难确定，而且方块的状态难表示，可以将初始时各个颜色相同的方块合并，只关心这些大块的颜色和长度，若用f[i][j]表示将[i,j]区间的砖块合并的最大价值，找不到不同状态间的直接递推关系，所以要用f[i][j][len]表示合并[i,j]，第j个后紧接着一个长为len的大块，有2种决策：把j和后面的len长大块合并，或者留下他们，找到前面[i,j]的另一个颜色相同的大块，三个一块消掉，这就把问题转换成递归式思想可以解决的问题，这里用记忆化DFS比较好写，不过一定要注意终止条件(DP的边界)——当这个方块的区间为1，即只有1个大块时，直接把这个大块和右边的相同颜色大块消除即可，还有要注意的是，题目有多组测试数据，每次要把记忆化数组清零！

#include <stdio.h>
#include <string.h>

#define MAXN 220

struct box //盒子
{
	int color,len; //盒子的颜色、长度
}segment[MAXN];

int score[MAXN][MAXN][MAXN]; //s[l][r][extra_len]表示第l-r个大块，右边紧接着长度为extra_len，与第r个大块颜色相同的大块，合并操作后获得的分数

int click_box(int l,int r,int extra_len) //获得第l-r个大块，右边紧接着长度为extra_len，与第r个大块颜色相同的大块，合并操作后获得的分数
{
	int result,i,temp;
	if(score[l][r][extra_len]) return score[l][r][extra_len];
	result=extra_len+segment[r].len;
	result*=result;
	if(l==r)
	{
		score[l][r][extra_len]=result;
		return result;
	}
	result+=click_box(l,r-1,0);
	for(i=r-1;i>=l;i--) //遍历找到一个与第r个大块颜色相同,且操作后获得分值最大的大块
	{
		if(segment[i].color!=segment[r].color) continue;
		temp=click_box(l,i,segment[r].len+extra_len)+click_box(i+1,r-1,0);
		if(temp<=result) continue;//结果不够优,跳过
		result=temp;
		break;
	}
	score[l][r][extra_len]=result;
	return score[l][r][extra_len];
}

int main()
{
	int t,x,i,j,n,end,clr;
	scanf("%d",&t);
	for(x=1;x<=t;x++)
	{
		end=1;
		scanf("%d%d",&n,&segment[end].color);
		segment[end].len=1;
		for(i=2;i<=n;i++)
		{
			scanf("%d",&clr);
			if(clr==segment[end].color) segment[end].len++; //如果新的块与之前大块颜色一样，该大块的长度+1
			else
			{
				segment[++end].color=clr; //否则新增一个大块
				segment[end].len=1;
			}
		}
		printf("Case %d: %d\n",x,click_box(1,end,0));
		memset(score,0,sizeof(score));
	}
	return 0;
}

[POJ 1390]Blocks,布布扣,bubuko.com

[POJ 1390]Blocks

标签：dp   记忆化dfs   

原文地址：http://blog.csdn.net/qpswwww/article/details/37915087