标签:
通常来说,要实现循环双向链表,每个节点需要有两个链域:前驱和后继。现在的问题是:如何设计一种环形表,使表的每个结点只包含一个链域而又能够有效地对其进行两个方向的查找。本文将给出一种实现方式。
首先,在给出之前,需要先了解一种有趣的运算,那就是异或运算。异或运算的真值表如下:
| A | B | A^B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
通过异或的性质可以知道,对于任意一个二进制数a,有a^a = 0。利用这一性质,考虑下面一个经典例子:实现两个整数的交换
void swap(int *x, int *y)
{
*y = *x ^ *y; /* step 1 */
*x = *x ^ *y; /* step 2 */
*y = *x ^ *y; /* step 3 */
}
为什么上述代码可以实现两个数的交换?以调用swap(&a, &b)为例,下表给出了解释:
| step | *x | *y |
| Initialization | a | b |
| step 1 | a | a^b |
| step 2 | a^a^b=0^b=b | a^b |
| step 3 | b | b^a^b=0^a=a |
是的,通过上表可以知道,利用a^a = 0,我们可以这样“高大上”的实现两个数的交换(事实上,这种交换方式并没有性能上的优势)。但是我们可以借助它来理解异或运算。通过上表我们更加可以总结出公式a^a^b = b。这对于本文要解决的问题有什么启示呢?
要使得表的每个结点只包含一个链域而又能够有效地对其进行两个方向的查找,可以让节点的链域存结点的前驱prev和后继next的异或,再利用异或运算的性质,可以得到(prev ^ next) ^ next = prev; (prev ^ next) ^ prev = next 。我们可以把异或的链域看成一把特殊的锁,它有两把不同的钥匙,用钥匙next就可以打开前驱prev的门,而用钥匙prev就可以打开后继next的门。
环形表的设计如下:
typedef struct Node *Position;
typedef Position RingList;
struct Node
{
int data;
Position prevXORnext; //前驱和后继的异或
};
在创建环形链表时,首先建立一个头节点rL,并申明节点指针prev和next,为了让头节点的链域可以直接指向第一个节点firstP,将prev初始化为0,由于0和某值的异或不会改变该值,故rL->prevXORnext = prev^next = 0^next。不过注意Position型不能直接做异或运算,需要强转为int型算出结果后再强转为Position型。(由于Position为结构体指针,指针的存储为四个字节即32位,本质上可以看成int型)
创建环形链表函数如下:
RingList CreateRingList(Position *prevNode, Position *nextNode)
{
RingList rL = new Node; //头结点
int x;
Position p = rL;
Position prev = 0; //初始头节点的异或就相当于next
Position next;
Position firstP = NULL, secondP = NULL;
int n = 0;
while (scanf("%d", &x) != EOF)
{
n++;
Position newP = new Node;
if (n == 1)
firstP = newP;
if (n == 2)
secondP = newP; //保存第二个节点的指针便于之后更新第一个节点
newP->data = x;
next = newP;
p->prevXORnext = (Position)((int)prev ^ (int)next);
prev = p;
p = newP;
}
//将尾指针的链域与第一个节点相关联
p->prevXORnext = (Position)((int)prev ^ (int)firstP);
//形成环后,更新第一个节点的链域
firstP->prevXORnext = (Position)((int)p ^ (int)secondP);
*prevNode = p;
*nextNode = secondP;
return rL;
}
如果我们要查找p结点的后继,只需要在之前临时保存p结点的前驱prev,然后令p = p->prevXORnext^prev,根据异或运算的性质可知当前p即为之前p的后继next。同理,如果要查找p结点的前驱,只需要在之前临时保存p结点的后继next,然后令p = p->prevXORnext^next,此时p即为之前p的前驱prev。
顺时针访问函数如下:
void ClockWise(RingList rL, Position prev2)
{
Position firstP = rL->prevXORnext;
Position prev1 = firstP;
printf("%d", firstP->data);
Position cur = (Position)((int)prev1->prevXORnext ^ (int)(prev2));
while (cur != firstP)
{
printf(" %d", cur->data);
prev2 = prev1;
prev1 = cur;
cur = (Position)((int)prev1->prevXORnext ^ (int)(prev2));
}
printf("\n");
}
逆时针访问函数如下:
void AntiClockWise(RingList rL, Position next2)
{
Position firstP = rL->prevXORnext;
Position next1 = firstP;
printf("%d", firstP->data);
Position cur = (Position)((int)next1->prevXORnext ^ (int)(next2));
while (cur != firstP)
{
printf(" %d", cur->data);
next2 = next1;
next1 = cur;
cur = (Position)((int)next1->prevXORnext ^ (int)(next2));
}
printf("\n");
}
下面是完整代码:

#include <cstdio>
using namespace std;
typedef struct Node *Position;
typedef Position RingList;
struct Node
{
int data;
Position prevXORnext;
};
void ClockWise(RingList rL, Position prev2); //顺时针
void AntiClockWise(RingList rL, Position next); //逆时针
RingList CreateRingList(Position *prev, Position *next); //创建环形链表
int main()
{
Position prev, next;
RingList rL = CreateRingList(&prev, &next);
printf("顺时针:");
ClockWise(rL, prev);
printf("逆时针:");
AntiClockWise(rL, next);
return 0;
}
RingList CreateRingList(Position *prevNode, Position *nextNode)
{
RingList rL = new Node; //头结点
int x;
Position p = rL;
Position prev = 0; //初始头节点的异或就相当于next,而0异或某个数等于它本身
Position next;
Position firstP = NULL, secondP = NULL;
int n = 0;
while (scanf("%d", &x) != EOF)
{
n++;
Position newP = new Node;
if (n == 1)
firstP = newP;
if (n == 2)
secondP = newP; //保存第二个节点的指针便于之后更新第一个节点
newP->data = x;
next = newP;
p->prevXORnext = (Position)((int)prev ^ (int)next);
prev = p;
p = newP;
}
//将尾指针的链域与第一个节点相关联
p->prevXORnext = (Position)((int)prev ^ (int)firstP);
//形成环后,更新第一个节点的链域
firstP->prevXORnext = (Position)((int)p ^ (int)secondP);
*prevNode = p;
*nextNode = secondP;
return rL;
}
void ClockWise(RingList rL, Position prev2)
{
Position firstP = rL->prevXORnext;
Position prev1 = firstP;
printf("%d", firstP->data);
Position cur = (Position)((int)prev1->prevXORnext ^ (int)(prev2));
while (cur != firstP)
{
printf(" %d", cur->data);
prev2 = prev1;
prev1 = cur;
cur = (Position)((int)prev1->prevXORnext ^ (int)(prev2));
}
printf("\n");
}
void AntiClockWise(RingList rL, Position next2)
{
Position firstP = rL->prevXORnext;
Position next1 = firstP;
printf("%d", firstP->data);
Position cur = (Position)((int)next1->prevXORnext ^ (int)(next2));
while (cur != firstP)
{
printf(" %d", cur->data);
next2 = next1;
next1 = cur;
cur = (Position)((int)next1->prevXORnext ^ (int)(next2));
}
printf("\n");
}
运行结果如下:
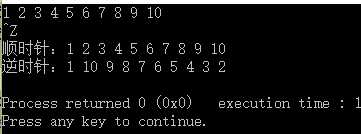
参考资料:《深入理解计算机系统》
(题外话:今天貌似是一个自发的程序员节:1024,虽然自己还是一个准程序员,也要祝自己节日快乐~hh~。希望在变成真正程序员之前这个节日能真正确定下来(●‘?‘●))
标签:
原文地址:http://www.cnblogs.com/llhthinker/p/4907552.html