标签:
拉格朗日乘子(Lagrange Multipliers)又称为待定乘数法(Undetermined Multipliers),通常用来寻找某一函数在一个或多个约束条件下的最值点。
其主要思想是引入一个新的变量λ(即拉格朗日乘子),把约束条件和原函数结合到一起,形成新的函数,这个新的函数的最值点与原函数相同。
本文内容主要来自《Pattern Recognition and Machine Learning》和和Andrew Ng的CS229讲义。
第一个问题
假设我们有一个函数f(x1,x2) ,现在我们要在约束条件 g(x1,x2)=0的约束下求函数f(x1,x2)的最大值。
最简单的做法是,我们先对函数g进行变换,成为 x2 = h(x1) 的形式,然后把 h(x1) 作为x2 代入函数f,f(x1, x2)就变成了 f(x1,h(x1)) ,即仅与 x1 相关的函数,这时候我们就可以通过变换,求出 x1 的极致点,继而获得x2的极致点 x2 = h(x1)。
这种方法的的缺点是,某些函数中的变量如x2可能不那么容易找到其对应的x1变换,而且这种方法也把x1和x2按照不同的方式来处理,改变了他们的自然对称。
更优雅的方式
现在,我们来看一种更优雅的,被成为拉格朗日乘子法的方法,我们需要引入一个 λ 变量,该变量即拉格朗日乘子。
我们最好从几何学的角度来学习这种方法:假设我们有一个一个D维的变量x(每一维分别是x1,x2,x3 ... xD),那么约束条件 g(x) = 0 就代表了一个D-1 维度的超平面:
假设现在平面 g(x) = 0上有非常接近的两个点 x + e和 x ,且 g(x)平面的梯度(gradient)为 ∇g(x) ,那么有:
由于x和x+e非常接近,那么我们可以认为 g(x+e) = g(x),继而有:
由于 e 是平行于 g(x)=0 平面的,所以 ∇g(x) 总是垂直于约束平面 g(x) = 0 。
更进一步
因此,最大值所在点的梯度 ∇f(x)与任一点所在的梯度 ∇g(x)必然是平行关系,所以有(其中λ != 0):
有上面的公式,我们可以引入拉格朗日公式为(对拉格朗日公式求偏导数倒推就是上面的式子):

{rock_cloud: 我的理解是,L取极值时,也就是L偏导为0,此时f偏导为0,也取到极值点,因此可以用L的极值点代表f的极值点。}
一个等值约束的例子
假设我们需要找到以下函数的极值:
约束条件为(等值约束):
把他们写为拉格朗日公式为:
由于拉格朗日的极值点必然在所有位置参数的一阶导数都为0的情况下,即:
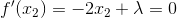

对上面三个公式求解,可以很容易得到(x1,x2) = (1/2,1/2)为极值点,并且λ = 1。
不等值约束
拉格朗日乘子法经过推广,可以一般化写为:
其中,目标函数,约束条件分别为:
也就是说,约束条件有多少个,就需要多少个拉格朗日乘子,即上面的

和

。
我们只讨论凸函数,即二次函数问题,非凸函数问题更加复杂,所以一般会把优化问题修改成凸函数优化问题。
现在再来看之前那个函数,求下面函数的最大值:
我们把约束条件改为:
现在,约束条件可以分为两部分,第一部分是 g(x1,x2) > 0,第二部分为 g(x1,x2) = 0。
对于第一部分来说,由于我们的目标函数是凹函数(可以转换为凸函数),所以在g(x1,x2)大于0的空间范围内,f(x1,x2)的极值只可能取在f(x1,x2)的导函数为0的时候,即 ∇f(x) = 0,也就是转换成拉格朗日函数之后把 λ = 0 。
对于第二部分 g(x1,x2) = 0 来说,只有当f(x1,x2)的梯度往g(x1,x2) > 0区域外移动的时候才可能取到最大值,在该最大值点有 ∇f(x) = −λ∇g(x) 。
对于这两种情况来说,最终都会导致 λg(x1,x2) = 0 (前者λ=0后者g(x1,x2))=0),所以原问题中在求f函数的最大值问题就转变成了在以下条件下求拉格朗日公式的最优值:
- g(x1,x2) >= 0
- λ >= 0
- λg(x1,x2) = 0
即,假如我们要求 f(x1,x2) 的最大值,只需在上面约束的情况下求拉格朗日函数的最大值即可(即对拉格朗日函数分别求x1,x2和λ求偏导数,让偏导数等于0)即可。
上面所述的三个条件,就是KKT条件,可以看做拉格朗日的推广。
拉格朗日对偶简介
标签:
原文地址:http://www.cnblogs.com/chenying99/p/4910178.html



 和
和 。
。