标签：
A schoolboy named Vasya loves reading books on programming and mathematics. He has recently read an encyclopedia article that described the method of median smoothing (or median filter) and its many applications in science and engineering. Vasya liked the idea of the method very much, and he decided to try it in practice.
Applying the simplest variant of median smoothing to the sequence of numbers a1, a2, ..., an will result a new sequence b1, b2, ..., bnobtained by the following algorithm:
The median of a set of three numbers is the number that goes on the second place, when these three numbers are written in the non-decreasing order. For example, the median of the set 5, 1, 2 is number 2, and the median of set 1, 0, 1 is equal to 1.
In order to make the task easier, Vasya decided to apply the method to sequences consisting of zeros and ones only.
Having made the procedure once, Vasya looked at the resulting sequence and thought: what if I apply the algorithm to it once again, and then apply it to the next result, and so on? Vasya tried a couple of examples and found out that after some number of median smoothing algorithm applications the sequence can stop changing. We say that the sequence is stable, if it does not change when the median smoothing is applied to it.
Now Vasya wonders, whether the sequence always eventually becomes stable. He asks you to write a program that, given a sequence of zeros and ones, will determine whether it ever becomes stable. Moreover, if it ever becomes stable, then you should determine what will it look like and how many times one needs to apply the median smoothing algorithm to initial sequence in order to obtain a stable one.
The first input line of the input contains a single integer n (3 ≤ n ≤ 500 000) — the length of the initial sequence.
The next line contains n integers a1, a2, ..., an (ai = 0 or ai = 1), giving the initial sequence itself.
If the sequence will never become stable, print a single number - 1.
Otherwise, first print a single integer — the minimum number of times one needs to apply the median smoothing algorithm to the initial sequence before it becomes is stable. In the second line print n numbers separated by a space — the resulting sequence itself.
4
0 0 1 1
0
0 0 1 1
In the second sample the stabilization occurs in two steps: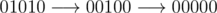 
, and the sequence 00000 is obviously stable.
题意：给你一个n的01串，在一次变换中a[i]=(a[i-1],a[i],a[i+1])的中值，问你经过几次变换，使得a稳定；
题解：我们列举可以发现只有 01010...,1010...,才会变换，对于长度len为偶数 变换次数就是 （len-1）/2;
对于奇数只能变为 00000或者11111....
对于偶数只能变为 000111或者111000...
所以我们遍历一遍就能找到答案0(n)；
///1085422276 #include<bits/stdc++.h> using namespace std ; typedef long long ll; #define mem(a) memset(a,0,sizeof(a)) #define meminf(a) memset(a,127,sizeof(a)); #define inf 100000007 inline ll read() { ll x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){ if(ch==‘-‘)f=-1;ch=getchar(); } while(ch>=‘0‘&&ch<=‘9‘){ x=x*10+ch-‘0‘;ch=getchar(); }return x*f; } //**************************************** #define maxn 500000+5 int a[maxn],len; int main() { int n=read(); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } int ans=0; for(int i=2;i<n;i++){ int j=i; while(abs(a[j]-a[j-1])==1&&j<=n){ j++; }if(j-(i-1)<3)continue;//cout<<i-1<<" "<<j<<endl; if((j-(i-1))%2){ len=j-(i-1); ans=max(ans,(len-1)/2); for(int k=i;k<j;k++){ a[k]=a[i-1]; }i=j-1; }else { len=j-(i-1); ans=max(ans,(len-1)/2); for(int k=i;k<=len/2+i-2;k++){ a[k]=a[i-1]; } for(int k=len/2+i-1;k<j;k++){ a[k]=a[j-1]; } } }cout<<ans<<endl; for(int i=1;i<=n;i++){ cout<<a[i]<<" "; } return 0; }
Codeforces Round #327 (Div. 2)C. Median Smoothing 构造
标签：
原文地址：http://www.cnblogs.com/zxhl/p/4911834.html
