条件随机场(Conditional Random Fields)入门篇

标签：

1.1 引言

关系数据有两个特征： 1 待建模实体概率不独立。2 待建模的实体往往有很多特征可以帮助分类。例如，分类网页时，网页的文字信息可以提供很多信息，但网页间的超链接也可以帮助分类。[Tasker et al., 2012]

图模型是一种利用实体间概率依赖性的自然形式，通常，图模型用来表示联合分布P(x,y), y 表示的是期望的预测，x则表示可见的待待建模实体，类似于mechine learing的 输入x⁽ⁱ⁾与类标记y，但是对非独立变量的联合分布建模会很困难，因为根据乘法公式P(x,y) = P(x)*P(y|x),对P(x)建模时，由于x并非独立，所以要考虑其中的概率依赖关系，而不能像NavieBayes那样认为实体x是独立的，这样会损失很多有益于分类的信息。

针对以上问题的解决办法是直接对P(x|y)建模，这对于分类来说已经足够了，这正是CRF所采用的方法。CRF就是一个可用图模型表示的条件分布P(x|y),这样就会避开对x的建模，例如，在NLP领域，有用的特征包括相邻的词，bi-grams（例如 ： front word & word）前后缀，大小写，领域词，或来自词网的语义信息。最近CRFs在文本处理，生物学，计算机视觉上很火热。　　

文章结构：

1. 介绍近期关于CRF的训练与使用，介绍CRF特例liner-chain CRF，并把这些模型与图模型关联起来

2. 通用的CRF的应用，比如信息抽取，这个模型会对非结构的文本建立起联系。通用CRF可以捕获到距离很远的实体的依赖关系，而不像liner-chain CRF 

3.

1.2 图模型

1.2.1 定义

对一个随机变量集合V=X ∪ Y,假设X是可观测的输入变量集合，Y是一系列我们要预测的输出。对一个随机变量取值序列V‘^, 是由一系列随机变量的取值 v（v∈V）构成的，v 即可是离散也可连续，这里只讨论离散的情况。

关于符号表示：

---

 

随机变量X的可能取值记做x

对随机变量A ⊂ X 的可能取值记做x_A

1_{x=x‘} 表示当x=x‘ 成立时，取值为1，否则取值为0

一个图模型即对图分解后的概率分布族。图模型的主要思想是表达一些随机变量的分布，这些随机变量产生自仅仅依赖与少量变量的局部函数。给定集合A ⊂ V ，给定一个无向图模型，其分布可以写成：

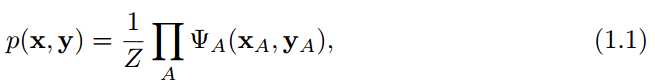
1.1中的F={φ_A}中的 φ_A = Vⁿ->R⁺(函数集合F又称作局部函数，或兼容函数)，偶然情况会使用随机场来描述无向图模型的分布，声明一下，本文中“模型”一词会经常用来概率分布族，而随机场则描述分布族中的一员。公式1.1中常量Z是一个正则化参数，计算如下：

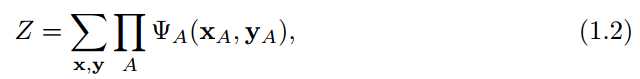
通常Z是很难计算的，但有许多方法可以近似计算。

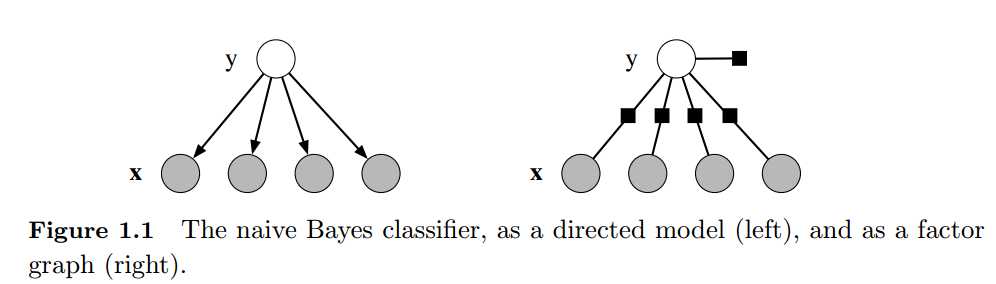
对公式1.1，可以用因子图的方式表示。因子图即二部图G=（V,E,F），其中若变量v是函数φ_A的参数，变量节点v_s∈V要与因子节点φ_A∈ F在图中是相连的。图1.1右边即为因子图的形式，图中圆形节点为变量节点，方形节点为因子节点

本文中，会假设每个局部函数形式如下：

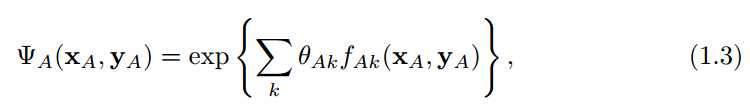
θ_A为实值参数，{f_Ak}为特征函数集合，这种形式确保了参数θ修饰的关于V的分布族是指数分布族，本文中所讨论的模型大部分都属于指数分布族。

无向图模型，贝叶斯网就基于无向图模型G=（V，E），无向图模型可以用如下公式表示：

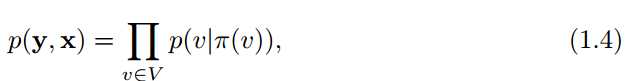
∏(v)在图G中是v的父节点，如图1.1所示。

术语“生成模型”描述的是无向图中输出变量拓扑产生输入变量，这就意味这，没有x∈X，可以是输出变量y∈Y的父节点，实际上，生成模型描述的正是输出变量如何依概率产生于输入变量。

1.2.2 图模型的应用

这章会详细阐述一些在NLP领域的应用，还会涉及到HMM，因为它与 liner-chain CRF密切相关。

1.2.2.1 分类

首先，对与分类问题，给定输入{x} = (x₁, x₂, . . . , x_k)，求输出y的类别，简单的解决办法就是假设{x}是独立的，而且类标签是已知的，如 Navie Bayes分类器就是这么处理的：

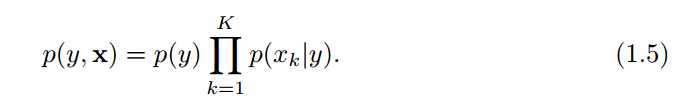
这个模型可以被表示中图1.1左边的形式

条件随机场(Conditional Random Fields)入门篇

标签：

原文地址：http://www.cnblogs.com/ooon/p/4867719.html