标签:
我们考虑一个$N\times M$的矩阵数据,若要对矩阵中的部分数据进行读取,比如求某个$a\times b$的子矩阵的元素和,通常我们可以想到$O(ab)$的遍历那个子矩阵,对它的各个元素进行求和。然而当$a$或$b$很大的时候,这样的计算显得太慢,如果要求子矩阵的最大元素和(如Ural 1146),更是简直慢到不能忍。
于是就想,能不能在读入数据的同时,我就先进行一些预处理,使得到后面进行计算的时候,可以简化一些步骤呢?答案是可以的。
通常对矩阵有两种预处理:
一种是把矩阵拍扁,即把前一列或前一行加到后一列或后一行上:
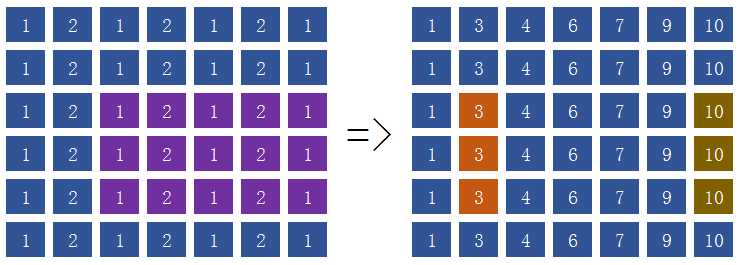
按列压缩↑,紫色部分和=棕色部分和-橙色部分和
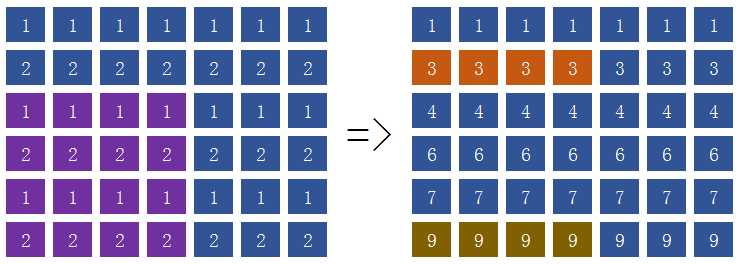
按行压缩↑,紫色部分和=棕色部分和-橙色部分和
开一个二维数组存放矩阵,第$0$行和第$0$列全都置$0$,我们真正的矩阵在数组中下标从$1$开始。
以按行压缩为例,读入当前元素$t=A_{ij}$后,我们令$B_{ij}=A_{ij}+B_{i-1,j}$,以此类推,当所有数据读入后,预处理即完成,$B_{ij}$表示对于矩阵$A$的第$j$列,从第$1$行到第$i$行的和。这样我们若想要知道矩阵$A$第$j$列上,从第$p$行到第$q$行的和,直接用$B_{qj}-B_{p-1,j}, (p<=q)$一步求出,而不需要进行$q-p+1$步计算,那么从左上角$A_{ab}$到右下角$A_{ij}$的子矩阵元素和为\$sum=\sum_{p=a}^{i}\sum_{q=b}^{j}A_{pq}=\sum_{q=b}^{j}B_{iq}-\sum_{q=b}^{j}B_{a-1,q}\$,大大减少了计算量,降低了时间复杂度。
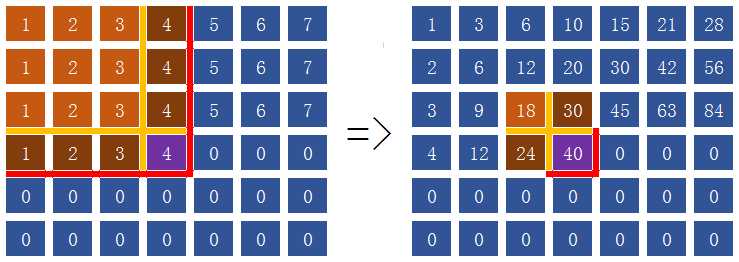
读入预处理↑,右图紫色块=4+24+30-18=40
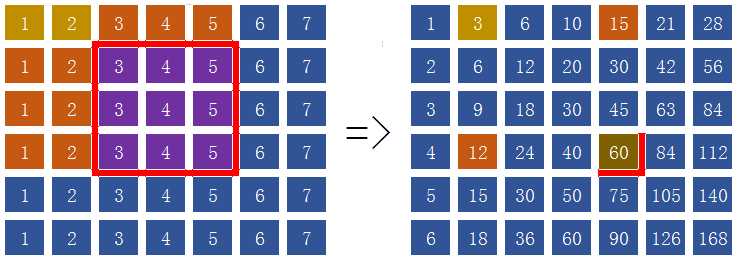
计算区域和↑,紫色区域和=60-12-15+3=36
而另一种则是压缩到一个元素上,用$B_{ij}$表示从最左上角元素$A_{11}$到元素$A_{ij}$的和$\sum_{p=1}^{i}\sum_{q=1}^{j}A_{ij}, (i \geq 1, j \geq 1)$,为了保持这一性质,我们在读入当前元素$t=A_{ij}$后,令$B_{ij}=A_{ij}+B_{i,j-1}+B_{i-1,j}-B_{i-1,j-1}$。当所有数据读入后,预处理即完成。我们若想要求出从左上角$A_{ab}$到右下角$A_{ij}$的子矩阵元素和,只需三步计算即可:sum=$\sum_{p=a}^{i}\sum_{q=b}^{j}A_{pq}$=$B_{ij}-B_{i,b-1}-B_{a-1,j}+B_{a-1,b-1}$,使时间复杂度降低到常数。
ACM 中 矩阵数据的预处理
标签:
原文地址:http://www.cnblogs.com/BlackStorm/p/4922207.html