标签:
一、问题描述
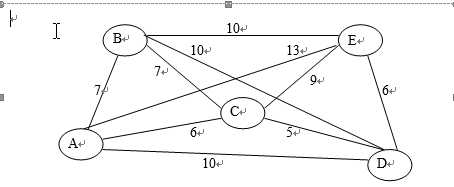
如图所示,一个旅行商从A点出发,需要不重复地走遍5个城市ABCDE,最后回到A。每个城市之间的花费(即权值)如图所示,现在要求找出一条总花费最小的路径,即权值和为最小的路径。
二、 算法说明
1. 算法一: 登山法(贪心法)
即在每一个城市出发前比较接下来所能走的城市花费(权值),找出权值最小的走。
优缺点:由于只是在每个城市局部地考虑权值最小,但当走完所用城市后,所得到权值和不一定为最小,所以采用此算法得不到精确解,但此算法复杂度较低。
2. 算法二:穷举法(本程序采用此算法)
即计算出每条路径的权值和,选权值和最小的路径为最佳路径。
优缺点:此算法可以得到精确解,但由于采用的是穷举,所以复杂度较高。
三、源码示例

1 using System; 2 using System.Collections.Generic; 3 using System.Linq; 4 using System.Text; 5 using System.Threading.Tasks; 6 7 namespace 旅行商问题 8 { 9 class Program 10 { 11 static void Main(string[] args) 12 { 13 //权值矩阵 14 int[,] weightValue = new int[10, 10]; 15 //城市数量 16 int cityNum = 0; 17 //城市名称 18 string[] cityName = new string[10]; 19 //出发城市 用索引表示 20 int beginCityIndex = 0; 21 //权值 22 int minWeightValue = int.MaxValue; 23 int weightSum = minWeightValue; 24 //最佳路径 25 int[] bestWay; 26 27 //输入城市数量 28 Console.WriteLine("请输入城市数量:"); 29 cityNum = int.Parse(Console.ReadLine()); 30 Console.WriteLine("请输入各个城市名称"); 31 for (int i = 0; i < cityNum; i++) 32 { 33 cityName[i] = Console.ReadLine(); 34 } 35 Console.WriteLine("请输入权值矩阵:"); 36 //输入权值矩阵 37 for (int i = 0; i < cityNum; i++) 38 { 39 for (int j = 0; j < cityNum; j++) 40 { 41 weightValue[i, j] = int.Parse(Console.ReadLine()); 42 } 43 } 44 //输入出发城市 45 Console.WriteLine("请输入出发城市:"); 46 beginCityIndex = int.Parse(Console.ReadLine()); 47 48 bestWay = new int[cityNum+1]; 49 50 for (int i = 0; i < cityNum; i++) 51 { 52 if (i != beginCityIndex) 53 { 54 for (int j = 0; j < cityNum; j++) 55 { 56 if (j != i && j != beginCityIndex) 57 { 58 for (int k = 0; k < cityNum; k++) 59 { 60 if(k!=j && k!=i && k!=beginCityIndex) 61 { 62 for (int t = 0; t < cityNum; t++) 63 { 64 if(t!=i && t!=j && t!=k && t!=beginCityIndex) 65 { 66 weightSum = weightValue[beginCityIndex,i] 67 +weightValue[i,j] 68 +weightValue[j,k] 69 +weightValue[k,t] 70 +weightValue[t,beginCityIndex]; 71 if(minWeightValue>weightSum) 72 { 73 minWeightValue=weightSum; 74 bestWay[0] = beginCityIndex; 75 bestWay[1] = i; 76 bestWay[2] = j; 77 bestWay[3] = k; 78 bestWay[4] = t; 79 bestWay[5] = beginCityIndex; 80 } 81 } 82 } 83 } 84 } 85 } 86 } 87 } 88 } 89 90 91 Console.WriteLine("最短路径为:"); 92 Console.WriteLine(cityName[bestWay[0]]+"->" 93 + cityName[bestWay[1]] + "->" 94 + cityName[bestWay[2]] + "->" 95 + cityName[bestWay[3]] + "->" 96 + cityName[bestWay[4]] + "->" 97 + cityName[bestWay[5]]); 98 99 Console.WriteLine("最小权值为{0}", minWeightValue); 100 101 Console.ReadKey(); 102 } 103 } 104 }
标签:
原文地址:http://www.cnblogs.com/zhangbaochong/p/4925691.html