标签:
有N件物品和一个容量为V的背包。第i件物品的重量是w[i],价值是v[i]。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。在选择装入背包的物品时,对于每种物品i,只能选择装包或不装包,不能装入多次,也不能部分装入,因此成为0-1背包问题。
形式化描述为:给定n个物品,背包容量C >0,重量 第i件物品的重量w[i]>0, 价值v[i] >0 , 1≤i≤n.要求找一n元向量(X1,X2,…,Xn,), Xi∈{0,1}, 使得 ∑(w[i] * Xi) ≤C,且∑ v[i] * Xi达最大.即一个特殊的整数规划问题。
数学描述为:
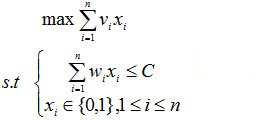
求解最优值:
设最优值m(i,j)为背包容量为j、可选择物品为i,i+1,……,n时的最优值(装入包的最大价值)。所以原问题的解为m(1,C)
将原问题分解为其子结构来求解。要求原问题的解m(1,C),可从m(n,C),m(n-1,C),m(n-2,C).....来依次求解,即可装包物品分别为(物品n)、(物品n-1,n)、(物品n-2,n-1,n)、……、(物品1,物品2,……物品n-1,物品n)。最后求出的值即为最优值m(1,C)。
若求m(i,j),此时已经求出m(i+1,j),即第i+1个物品放入和不放入时这二者的最大值。
对于此时背包剩余容量 j=0,1,2,3……C,分两种情况:
(1)当 w[i] > j ,即第i个物品重量大于背包容量j时,m(i,j)=m(i+1,j)
(2)当 w[i] <= j ,即第i个物品重量不大于背包容量j时,这时要判断物品i放入和不放入对m的影响。
若不放入物品i,则此时m(i,j)=m(i+1,j)
若放入物品i,此时背包剩余容量为 j-w[i],在子结构中已求出当容量k=0,1,2……C 时的最优值m(i+1,k)。所以此时m(i,j)=m(i+1,j-w[i])+v[i]。
取上述二者的最大值,即m(i,j) = max{ m(i+1,j),m(i+1,j-w[i])+v[i] }
总结得出状态转移方程为:
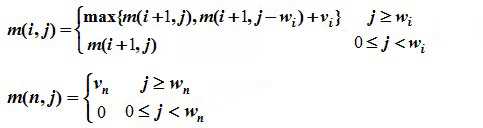
该算法的python代码实现:
1 # 0-1背包问题 2 __author__ = ‘ice‘ 3 4 5 # 背包容量0~capacity,不是0~capacity-1 6 def knapsack(weight, value, capacity): 7 if len(weight) != len(value): 8 print("parameter err!") 9 return 10 obj_num = len(weight) 11 result = [[] for x in range(obj_num)] 12 divide = min(weight[-1], capacity) 13 result[-1] = [0 for x in range(divide)] 14 result[-1].extend(value[-1] for x in range(divide, capacity + 1)) 15 for i in reversed(list(range(1, obj_num - 1))): 16 divide = min(weight[i], capacity) 17 for j in range(divide): 18 result[i].append(result[i + 1][j]) 19 for j in range(divide, capacity + 1): 20 result[i].append(max(result[i + 1][j], result[i + 1][j - weight[i]] + value[i])) 21 22 result[0] = {capacity: result[1][capacity]} 23 if weight[0] <= capacity: 24 result[0][capacity] = max(result[1][capacity], result[1][capacity - weight[0]] + value[0]) 25 26 vector = [0 for x in range(obj_num)] 27 capacity_temp = capacity 28 for i in range(obj_num - 1): 29 if result[i][capacity_temp] != result[i + 1][capacity_temp]: 30 vector[i] = 1 31 capacity_temp -= weight[i] 32 33 if capacity_temp == 0: 34 vector[-1] = 0 35 else: 36 vector[-1] = 1 37 38 return {‘total_value‘: result[0][capacity], ‘select‘: vector}
但是,但是!!该算法有两个明显的缺点:1,基于上述代码,因为数组索引的需要,要求所给物品重量为整数。2,当背包容量C很大时,算法所需计算时间较多。当C>2^n时,需要Ω(n*2^n)计算时间。
所以,所以!!改进算法如下:
对于函数m(i,j)的值,当i确定,j为自变量时,是单调不减的跳跃式增长,如图所示。而这些跳跃点取决于在(物品i,物品i+1,……物品n)中选择放入哪些物品使得在放入重量小于容量 j (0<=j<=C)的情况下m取得最大值。对于每一个确定的i值,都有一个对应的跳跃点集Pi={ ( j, m(i,j) ),……}。j始终小于等于C
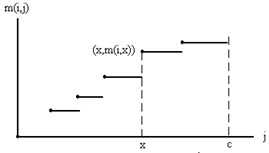
(1)开始求解时,先求Pi,初始时Pn+1={(0,0)},i=n+1,由此按下列步骤计算Pi-1,Pi-2……P1,即Pn,Pn-1,……P1
(2)求Qi,利用Pi求出m(i,j-w[i-1])+v[i-1],即Pi当放入物品i-1后的变化后的跳跃点集Qi={ ( j+w[i-1], m(i,j)+v[i-1] ),……},在函数图像上表现为所有跳跃点横轴坐标右移w[i-1],纵轴坐标上移v[i-1]。
(3)求Pi-1,即求Pi∪Qi然后再去掉受控跳跃点后的点集。此处有个受控跳跃点的概念:若点(a,b),(c,d)∈Pi∪Qi,且a<=c,b>d,则(c,d)受控于(a,b),所以(c,d)∉Pi-1。去掉受控跳跃点,是为了求得在物品i-1放入后m较大的点,即 使m取最优值的跳跃点。
由此计算得出Pn,Pn-1,……,P1。求得P1的最后那个跳跃点即为所求的最优值m(1,C)。
举个栗子:
n=5,c=10,w={2,2,6,5,4},v={6,3,5,4,6}。跳跃点的计算过程如下:
初始时p[6]={(0,0)}
因此,q[6]=p[6]⊕(w[5],v[5])={(4,6)}
p[5]={(0,0),(4,6)}
q[5]=p[5]⊕(w[4],v[4])={(5,4),(9,10)}
p[4]={(0,0),(4,6),(9,10)} p[5]与q[5]的并集p[5]∪q[5]={(0,0),(4,6),(5,4),(9,10)}中跳跃点(5,4)受控于跳跃点(4,6)。将受控跳跃点(5,4)清除后,得到p[4]
q[4]=p[4]⊕(6,5)={(6,5),(10,11)}
p[3]={(0,0),(4,6),(9,10),(10,11)}
q[3]=p[3]⊕(2,3)={(2,3),(6,9)}
p[2]={(0,0),(2,3),(4,6),(6,9),(9,10),(10,11)}
q[2]=p[2]⊕(2,6)={(2,6),(4,9),(6,12),(8,15)}
p[1]={(0,0),(2,6),(4,9),(6,12),(8,15)}
p[1]的最后的那个跳跃点(8,15)即为所求的最优值,m(1,C)=15
最后,python代码的实现:
1 class Point: 2 def __init__(self, x, y): 3 self.x = x 4 self.y = y 5 6 7 # 0-1背包问题 改进 8 def knapsack_improve(weight, value, capacity): 9 if len(weight) != len(value): 10 print("parameter err!") 11 return 12 obj_num = len(weight) 13 jump_points_p = [[] for x in range(obj_num)] 14 jump_points_q = [[] for x in range(obj_num)] 15 jump_points_p.append([Point(0, 0)]) 16 jump_points_q.append([Point(weight[obj_num - 1], value[obj_num - 1])]) 17 for i in reversed(list(range(1, obj_num))): 18 jump_points_p[i] = merge_points(jump_points_p[i + 1], jump_points_q[i + 1]) 19 for i in reversed(list(range(1, obj_num))): 20 jump_points_p[i] = merge_points(jump_points_p[i + 1], jump_points_q[i + 1]) 21 jump_points_q[i] = [Point(point.x + weight[i - 1], point.y + value[i - 1]) for point in jump_points_p[i] if 22 point.x + weight[i - 1] <= capacity] 23 result = merge_points(jump_points_p[1], jump_points_q[1]) 24 25 return result 26 27 28 def merge_points(points_x, points_y): 29 x_len = len(points_x) 30 y_len = len(points_y) 31 merged_points = [] 32 i = j = 0 33 while True: 34 if i == x_len or j == y_len: 35 break 36 if points_x[i].x < points_y[j].x: 37 merged_points.append(points_x[i]) 38 if points_x[i].y >= points_y[j].y: 39 j += 1 40 i += 1 41 else: 42 merged_points.append(points_y[j]) 43 if points_y[j].y >= points_x[i].y: 44 i += 1 45 j += 1 46 while i < x_len: 47 if points_x[i].x > merged_points[-1].x and points_x[i].y > merged_points[-1].y: 48 merged_points.append(points_x[i]) 49 i += 1 50 while j < y_len: 51 if points_y[j].x > merged_points[-1].x and points_y[j].y > merged_points[-1].y: 52 merged_points.append(points_y[j]) 53 j += 1 54 return merged_points 55 56 57 result = knapsack_improve([2, 2, 6, 5, 4], [6, 3, 5, 4, 6], 10) 58 print() 59 for point in result: 60 print(‘(‘ + str(point.x) + ‘,‘ + str(point.y) + ‘)‘, end=‘ ‘) 61 62 #(0,0) (2,6) (4,9) (6,12) (8,15)
标签:
原文地址:http://www.cnblogs.com/z941030/p/4925324.html