原题

http://acm.hit.edu.cn/hoj/problem/view?id=2901

Given two integers a and b, you are to calculate the value of the following expression: (1^b + 2^b + ... + a^b) modulo a.

Note that b is an odd number.

Input specifications

Each line of input consists of two integers a and b (1≤a≤1000000000, 1≤b≤1000000000) respectively.

Output specifications

For each case of input, you should output a single line, containing the value of the expression above.

Sample Input

1 1
2 1

Sample Output

  0

  1

思路

   快速幂模板题。

   中等难度是因为有一个人类根本YY不出来的优化：（我偷偷看了看题解。。）

        根据二项式展开，发现  [ c^b+(a-c)^b ] % a = 0 ，所以有：

                若a为奇数，答案为0，若a为偶数，答案为a/2的b次方（快速幂）  还要%a。。

   下面给个人类的推导过程：

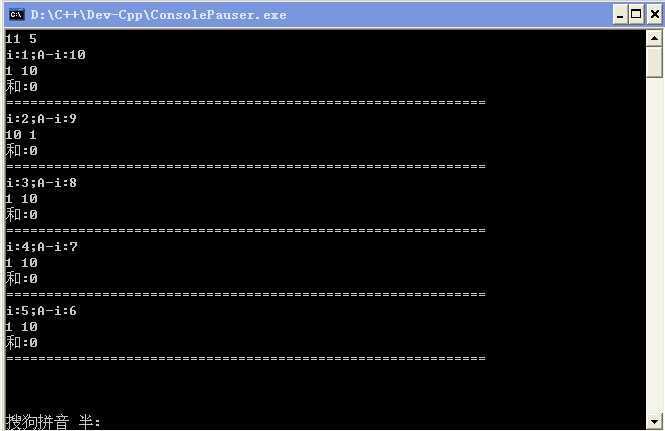
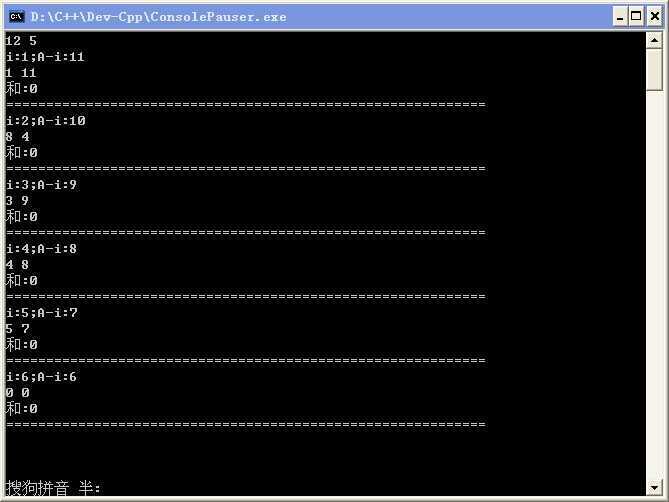
    一定是发现了什么不得了的东西：当我们把第i项和第A-i项的结果相加，刚好会被A整除。。所以。。

    只有偶数的一半那个（如上图12的一半6）只有两个自己相加。。而实际上没有两个同样的项，那么我们要输出的就是它的快速幂结果。。

    所以：奇数：0，偶数：（（A/2）^B）%A；

    这样我们成功把复杂度降到了O（n）左右。。（如果出题人太坑也没办法，事实证明没有这么坑）

    这里以上的证明都是针对B为奇数的特例，如果B为偶数则以上式子均不适用

    (如果A，B均为偶数，则第i项与第A-i+1项的和会呈现对称分布。。（或者说第i项与第A-i项的和们最后一项是0，前面的呈现对称分布)，

     而若A为奇数，B为偶数，第i项与第A-i（+1）项的和会很奇怪。。我也没找到规律。。)

注意

   一个数的奇偶性可以用&1来判断，即若（P&1）==1则表示P为奇数，若（P&1）==0则表示P为偶数

当然，这只是一个优化常数的方法。。如果没有把握还是用%2吧。。

代码

/*http://acm.hit.edu.cn/hoj/problem/view?id=2901*/

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
long long A,B;

inline int read()
{
    long long x=0,f=1;char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
    return x*f;
}


struct pointer
{
    long long AA,BB;
};

long long Matrix_multiplication(long long a, long long n)
{
    long long ret = 1;
    while(n)
    {
        if(n&1) ret = (ret*a)%A;
        a = (a*a)%A;
        n >>= 1;
    }
    return ret;
}

int main()
{
    long long times,ans;
    while( cin>>A>>B )
    {
    ans=0;
        if ((A&1)==0)
        {
          ans=Matrix_multiplication(A/2,B);
          ans%=A;
        }
        else 
        {
            ans=0;
        }
    cout<<ans<<endl;
}
    return 0;
}

结果