Description (描述)

After learning Chapter 1, you must have mastered the convex hull very well. Yes, convex hull is at the kernel of computational geometry and serves as a fundamental geometric structure. That‘s why you are asked to implement such an algorithm as the first of your programming assignments.

Specifically, given a set of points in the plane, please construct the convex hull and output an encoded description of all the extreme points.

经过了第一章的学习，想必你对于凸包的认识已经非常深刻。是的，凸包是计算几何的核心问题，也是一种基础性的几何结构。因此你的第一项编程任务，就是来实现这样的一个算法。

具体地，对于平面上的任意一组点，请构造出对应的凸包，并在经过编码转换之后输出所有极点的信息。

Input (输入)

The first line is an integer n > 0, i.e., the total number of input points.

The k-th of the following n lines gives the k-th point:

p_k = (x_k, y_k), k = 1, 2, ..., n

Both x_k and y_k here are integers and they are delimited by a space.

第一行是一个正整数首行为一个正整数n > 0，即输入点的总数。

随后n行中的第k行给出第k个点：

p_k = (x_k, y_k), k = 1, 2, ..., n

这里，x_k与y_k均为整数，且二者之间以空格分隔。

Output (输出)

Let { s₁, s₂, ..., s_h } be the indices of all the extreme points, h ≤ n. Output the following integer as your solution:

( s₁ * s₂ * s₃ * ... * s_h * h ) mod (n + 1)

若 { s₁, s₂, ..., s_h } 为所有极点的编号, h ≤ n，则作为你的解答，请输出以下整数：

( s₁ * s₂ * s₃ * ... * s_h * h ) mod (n + 1)

Sample Input (输入样例)

10
7 9
-8 -1
-3 -1
1 4
-3 9
6 -4
7 5
6 6
-6 10
0 8

Sample Output (输出样例)

7   // ( 9 x 2 x 6 x 7 x 1 x 5 ) % (10 + 1)

Limitation (限制)

• 3 ≤ n ≤ 10^5
• Each coordinate of the points is an integer from (-10^5, 10^5). There are no duplicate points. Each radom point is selected uniformly in (-10^5, 10^5) x (-10^5, 10^5).
• All points on extreme edges are regarded as extreme points and hence should be included in your solution.
• Time Limit: 2 sec
• Space Limit: 512 MB

• 3 ≤ n ≤ 10^5
• 所有点的坐标均为范围(-10^5, 10^5)内的整数，且没有重合点。每个点在(-10^5, 10^5) x (-10^5, 10^5)范围内均匀随机选取
• 极边上的所有点均被视作极点，故在输出时亦不得遗漏
• 时间限制：2 sec
• 空间限制：512 MB

Hint (提示)

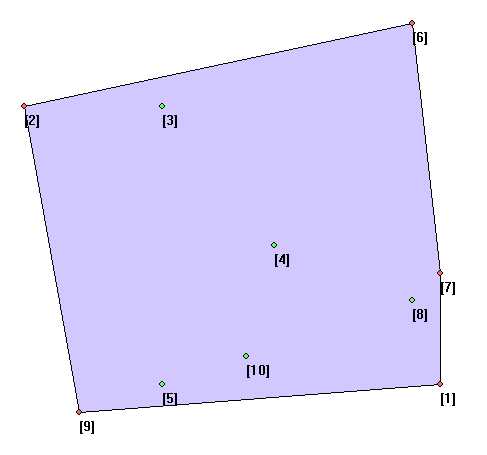
CH algorithms presented in the lectures

课程中讲解过的凸包算法

真TM历经波折啊。。。一直找不到坑在哪？

题意：求凸包极点个数，然后求一表达式。

题解：Andrew  水平序扫描，O（logn）。

坑点：

1.注意共线情况：只需将小于等于变为小于保留共线情况即可。

#include<stdio.h>
#include<algorithm>
using namespace std;
const int MAX=100000+5;
typedef long long LL;
int n;
struct Point
{
    LL x,y;
    int pos;
    Point(LL x=0,LL y=0,int p=0):x(x),y(y),pos(p) {}
} p[MAX],ch[MAX];
typedef Point Vector;
Vector operator + (Vector A, Vector B)
{
    return Vector(A.x + B.x, A.y + B.y);
}
Vector operator - (Vector A, Vector B)
{
    return Vector(A.x - B.x, A.y - B.y);
}
bool operator == (const Vector& A, const Vector& B)
{
    return A.x-B.x==0 && A.y-B.y==0;
}
LL Cross(Vector A, Vector B)
{
    return A.x * B.y - A.y * B.x;
}
bool cmp(Point A, Point B)
{
    if(A.x != B.x)	return A.x < B.x;
    else return A.y < B.y;
}
int ConvexHull()
{
    sort(p+1,p+n+1,cmp);
    int m = 0;
    for(int i = 1; i <= n; i++)
    {
        while(m > 1 && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) < 0) m--;
        ch[m++] = p[i];
    }
    if(m==n) return n;
    int k = m;
    for(int i = n-1; i >=1; i--)
    {
        while(m > k &&Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) < 0) m--;
        ch[m++] = p[i];
    }
    if(n > 1) m--;
    return m;
}
int main()
{
    int m;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i = 1; i <= n; i++)
        {
            LL a,b;
            scanf("%lld%lld",&a,&b);
            p[i] = Point(a,b,i);
        }
        m = ConvexHull();
        //printf("%d\n",m);
        LL ans=1;
        for(int i=0; i<m; i++)
            ans=((ans%(n+1))*(ch[i].pos%(n+1)))%(n+1);
        ans=((ans%(n+1))*(m%(n+1)))%(n+1);
        printf("%lld\n",ans);
    }
    return 0;
}