标签:
定义: a,b,c是整数,且ab!=0,那么形如ax+by=c的方程称为二元一次不定方程
定理1: 设a,b是整数且 d = gcd(a,b) 如果d|c,那么返程存在无穷多个整数解,否则不存在整数解。
这里大概可以发现二元一次不定方程和同余方程可以相互转化,如在a>0且b>0的条件下,求二元一次方程ax+by=c整数解等价于求一元线性同余方程ax≡c(mod b)的整数解。
给出poj 2142这个题练练手
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 5225 | Accepted: 2297 |
Description
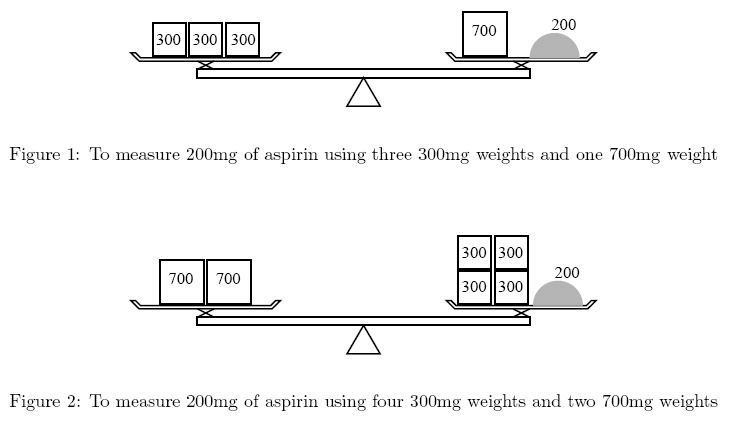
Input
Output
Sample Input
700 300 200 500 200 300 500 200 500 275 110 330 275 110 385 648 375 4002 3 1 10000 0 0 0
Sample Output
1 3 1 1 1 0 0 3 1 1 49 74 3333 1
Source

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 5 using namespace std; 6 7 int gcd(int a,int b) 8 { 9 if(b == 0) return a; 10 else return gcd(b,a%b); 11 } 12 13 14 int ex_gcd(int a,int b,int &x,int &y) 15 { 16 if(b == 0){ 17 x = 1; 18 y = 0; 19 return a; 20 } 21 else { 22 ex_gcd(b,a%b,x,y); 23 int t = x; 24 x = y; 25 y = t - a/b*y; 26 return t; 27 } 28 } 29 30 int main() 31 { 32 int a,b,c,x,y; 33 while(scanf("%d%d%d",&a,&b,&c)!=EOF){ 34 if(a == 0 && b == 0 && c == 0) break; 35 int d = gcd(a,b); 36 a /= d; 37 b /= d; 38 c /= d; 39 ex_gcd(a,b,x,y); 40 int xx = x*c; 41 xx = (xx%b+b)%b; 42 int yy = (c - a*xx)/b; 43 if(yy < 0) yy = -yy; 44 y = y*c; 45 y = (y%a+a)%a; 46 x = (c - b*y)/a; 47 if(x < 0) x = -x; 48 if(x+y > xx+yy){ 49 x = xx; 50 y = yy; 51 } 52 printf("%d %d\n",x,y); 53 } 54 55 return 0;
标签:
原文地址:http://www.cnblogs.com/lmlyzxiao/p/4937351.html