标签:style blog http color strong os
重拾算法(2)——线索二叉树
上一篇我们实现了二叉树的递归和非递归遍历,并为其复用精心设计了遍历方法Traverse(TraverseOrder order, NodeWorker<T> worker);今天就在此基础上实现线索二叉树。
二叉树中容易找到结点的左右孩子信息,但该结点在某一序列中的直接前驱和直接后继只能在某种遍历过程中动态获得。
先依遍历规则把每个结点某一序列中对应的前驱和后继线索预存起来,这叫做"线索化"。
意义:从任一结点出发都能快速找到其某一序列中前驱和后继,且不必借助堆栈。
这就是线索二叉树(Threaded Binary Tree)
如何预存这类信息?有两种解决方法。

任意一个二叉树,其结点数为N,则有N+1个空链域。空链域就是叶结点的lchild和rchild。比如下面这个二叉树
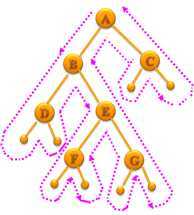
它有7个结点,有(7+1)个空链域。这个结论可以用数学归纳法证明。
大体思路就是充分利用那n+1个空链域,用它存储前驱结点和后继结点。
我们规定:
那么就有如下一个问题:如何判断是孩子指针还是线索指针?

容易的很,加两个标志域:
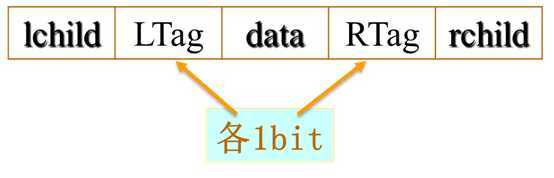
标志域只需要2个bit,而用增加指针域的方式则需要2个指针的空间(一个指针就是一个int的长度)。所以这个方案极大地节省了空间。
我们规定:
线索链表:用含Tag的结点样式所构成的二叉链表。
线 索:指向结点前驱和后继的指针。
线索二叉树:加上线索的二叉树。
线 索 化:对二叉树以某种次序遍历使其变为线索二叉树的过程。
线索化过程就是在遍历过程中修改空指针的过程:
线索二叉树是(is a)二叉树。所以最初我想继承上一篇的二叉树BinaryTreeNode<T>类型。但后来发现代码不太好掌控,不如来得直接些,让二叉树和线索二叉树作为两个毫不相干的类型。以后重构的时候再考虑考虑如何整合。
1 public partial class ThreadedBinaryTreeNode<T> 2 { 3 public T Value { get;set; } 4 public ThreadedBinaryTreeNode<T> Parent { get;set; } 5 public ThreadedBinaryTreeNode<T> Left { get;set; } 6 public ThreadedBinaryTreeNode<T> Right { get;set; } 7 public bool Point2PreviousNode { get; private set; } 8 public bool Point2NextNode { get; private set; } 9 public TraverseOrder Order { get;set; } 10 private bool threadedOnce = false; 11 12 public ThreadedBinaryTreeNode(T value, ThreadedBinaryTreeNode<T> parent = null, ThreadedBinaryTreeNode<T> left = null, ThreadedBinaryTreeNode<T> right = null) 13 { 14 this.Value = value; this.Parent = parent; this.Left = left; this.Right = right; 15 } 16 17 public void Traverse(TraverseOrder order, ThreadedNodeWorker<T> worker) 18 { 19 if (worker == null) { return; } 20 21 if ((!threadedOnce) || (order != this.Order)) 22 { 23 var router = new Router<T>(worker); 24 this.NormalTraverse(order, router); 25 this.Order = order; 26 this.threadedOnce = true; 27 } 28 else 29 { 30 this.ThreadedTraverse(order, worker); 31 } 32 } 33 } 34 35 public abstract class ThreadedNodeWorker<T> 36 { 37 public abstract void DoActionOnNode(ThreadedBinaryTreeNode<T> node); 38 }
C#里用bool类型作为标志变量大概再好不过了。
线索二叉树的线索化是首先要解决的问题。
1 public partial class ThreadedBinaryTreeNode<T> 2 { 3 /* 略 */ 4 private void RefreshThread(TraverseOrder order) 5 { 6 var threader = new Threader<T>(); 7 this.NormalTraverse (order, threader); 8 this.Order = order; 9 } 10 11 class Threader<TThreader> : ThreadedNodeWorker<TThreader> 12 { 13 Queue<ThreadedBinaryTreeNode<TThreader>> queue = new Queue<ThreadedBinaryTreeNode<TThreader>>(); 14 public override void DoActionOnNode(ThreadedBinaryTreeNode<TThreader> node) 15 { 16 this.queue.Enqueue(node); 17 if (this.queue.Count <= 1) { return; } 18 19 var pre = this.queue.Dequeue(); 20 var next = this.queue.Peek(); 21 if (pre.Right == null) 22 { 23 pre.Right = next; 24 pre.Point2NextNode = true; 25 } 26 if (next.Left == null) 27 { 28 next.Left = pre; 29 next.Point2PreviousNode = true; 30 } 31 } 32 } 33 }
代码中的this.NormalTraverse()函数与上一篇中二叉树的遍历方法Traverse()思路是一样的,唯一区别在于传入的操作结点的对象threader,这个threader在用前序、中序、后序或层次遍历二叉树时,将结点存入一个队列queue,当queue中有2个结点时,就设置他们互为前驱后驱(若此2个结点的Left/Right为空的前提下)。简单来说,就是遍历二叉树,根据访问结点的先后顺序依次修改其前驱后驱指针(及标识)
完成线索化后,就可以遍历了。
前序遍历线索二叉树的思路是:对于一个结点A及其左右子树Left和Right,先访问A;如果A的标记Point2NextNode为true,则A的下一结点通过A.Right就能确定;否则,有两种情况:(1)A的下一结点在A.Left上,而以A.Left为根的这个子树的第一个被访问的结点,恰恰是A.Left这个结点。(2)A.Left为空,这说明A的下一结点在A.Right上。若A.Right也为空,就说明整个树遍历结束。
1 void ThreadedPreorderTraverse(ThreadedNodeWorker<T> worker) 2 { 3 var node = this;// root node is the first node to work with. 4 while (node != null) 5 { 6 worker.DoActionOnNode(node); 7 if (node.Point2NextNode) 8 { 9 node = node.Right; 10 } 11 else 12 { 13 if (node.Left != null)// visit left sub tree 14 { 15 node = node.Left;// first node of left sub tree is the ‘root‘ of left sub tree 16 } 17 else 18 { 19 node = node.Right;// node.Right cannot be null because the tree is threaded. 20 // Only one condition can break this when node.Right is the last node to visit. 21 } 22 } 23 } 24 }
中序遍历线索二叉树的思路是:对于一个结点A及其左右子树Left和Right,第一个要访问的结点在A.Left子树,A.Left子树中第一个要访问的结点则在A.Left.Left子树中,依次循环,直到最后一个叶结点的Left。所以A树要访问的第一个结点就用GetLeftMostNode()这个函数去找。访问完A,就该A的右子树了,所以A.Right就成为下一个A了,所以就用GetLeftMostNode(A.Right)获取下一个结点。
1 ThreadedBinaryTreeNode<T> GetLeftMostNode(ThreadedBinaryTreeNode<T> node) 2 { 3 if (node == null) { return null; } 4 while (node.Left != null) 5 { 6 node = node.Left; 7 } 8 return node; 9 } 10 11 void ThreadedInorderTraverse(ThreadedNodeWorker<T> worker) 12 { 13 var node = GetLeftMostNode(this); 14 while (node != null) 15 { 16 worker.DoActionOnNode(node); 17 if (node.Point2NextNode) 18 { 19 node = node.Right; 20 } 21 else 22 { 23 node = GetLeftMostNode(node.Right);// visit right sub tree. 24 } 25 } 26 }
后序遍历线索二叉树的思路是:对于一个结点A及其左右子树Left和Right,第一个要访问的结点在A.Left子树,A.Left子树中第一个要访问的结点则在A.Left.Left子树中,依次循环,直到最后一个叶结点的Left。所以A树要访问的第一个结点就用GetLeftMostNode()这个函数去找。访问完A树,下一步分三种情况:(1)A是整个树的根,这时整个遍历结束。(2)A树是A.Parent的左子树,这时就该A.Parent.Right了,于是A.Parent.Right就成了之前的A。(3)A树是A.Parent的右子树,这时就该A结点了。
1 void ThreadedPostorderTraverse(ThreadedNodeWorker<T> worker) 2 { 3 var node = GetLeftMostNode(this); 4 while (node != null) 5 { 6 worker.DoActionOnNode(node); 7 if (node.Point2NextNode) 8 { 9 node = node.Right; 10 } 11 else 12 { 13 var parent = node.Parent; 14 if (parent != null)// node is NOT root 15 { 16 if (parent.Right == node)// node is right sub tree of parent 17 { 18 node = parent; 19 } 20 else// node is left sub tree of parent 21 { 22 node = GetLeftMostNode(parent.Right);//parent.Right will never be null because the tree is threaded. 23 } 24 } 25 else// node is root of whole tree 26 { 27 node = parent; 28 } 29 } 30 } 31 }
线索二叉树对于层次遍历似乎没有优化的能力,其层次遍历仍旧用普通二叉树的遍历方法好了。
1 void ThreadedLayerTraverse(ThreadedNodeWorker<T> worker) 2 { 3 NormalLayerTraverse(worker); 4 } 5 void NormalLayerTraverse(ThreadedNodeWorker<T> worker) 6 { 7 var queue = new Queue<ThreadedBinaryTreeNode<T>>(); 8 queue.Enqueue(this); 9 while (queue.Count > 0) 10 { 11 var element = queue.Dequeue(); 12 if (element != null) 13 { 14 worker.DoActionOnNode(element); 15 var left = element.Left; 16 var right = element.Right; 17 if (left != null) { queue.Enqueue(left); } 18 if (right != null) { queue.Enqueue(right); } 19 } 20 } 21 }
学习了线索二叉树后,我对算法思维有了新的认识。在想一个子问题的时候,以不同的角度思考,得到不同的结论,将其连接起来,竟然能够得到整个问题的解。
标签:style blog http color strong os
原文地址:http://www.cnblogs.com/bitzhuwei/p/algorithm-2-threaded-binary-tree.html