标签:
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 521 Accepted Submission(s): 125
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #define eps 1e-8 7 #define PI acos(-1.0) 8 #define LL long long 9 #define maxn 100100 10 #define IN freopen("in.txt","r",stdin); 11 using namespace std; 12 13 14 struct Point { 15 double x,y; 16 }; 17 18 int sign(double x) { 19 if(fabs(x)<eps) return 0; 20 return x<0? -1:1; 21 } 22 23 double Distance(Point p1,Point p2) { 24 return sqrt((p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y)); 25 } 26 27 28 int n; 29 Point p[maxn]; 30 double d[maxn]; 31 32 int check(double r) 33 { 34 if(sign(r) < 0) return 0; 35 36 for(int i=2 ;i<=n; i++) { 37 r = d[i]-r; 38 if(sign(r) < 0) return 0; 39 } 40 return 1; 41 } 42 43 44 /*三分法求面积最小时的r*/ 45 double a,b,c; 46 double cal(double x) { 47 return a*x*x + b*x + c; 48 } 49 50 double solve(double low, double high) 51 { 52 while(high-low > eps){ 53 double mid = (high+low)/2.0; 54 double midmid = (mid+high)/2.0; 55 if(sign(cal(midmid)-cal(mid)) > 0) high = midmid; 56 else low = mid; 57 } 58 59 return low; 60 } 61 62 63 int main(int argc, char const *argv[]) 64 { 65 //IN; 66 67 int t;scanf("%d",&t); 68 while(t--) 69 { 70 double r = 0; 71 memset(p, 0, sizeof(p)); 72 memset(d, 0, sizeof(d)); 73 int flag = 1; 74 75 scanf("%d", &n); 76 for(int i=1 ;i<=n; i++) 77 scanf("%lf %lf", &p[i].x, &p[i].y); 78 d[1]=Distance(p[1], p[n]); 79 for(int i=2; i<=n; i++) 80 d[i] = Distance(p[i], p[i-1]); 81 82 if(n%2 != 0){ 83 r = d[1]; 84 for(int i=2; i<=n; i++){ 85 if(i%2 == 0) r += d[i]; 86 else r -= d[i]; 87 } 88 r /= 2.0; 89 flag = check(r); 90 } 91 92 else{ 93 double tmp = 0; 94 for(int i=1; i<=n; i++){ 95 if(i%2 != 0) tmp += d[i]; 96 else tmp -= d[i]; 97 } 98 if(sign(tmp) != 0) {flag=0; goto end;} 99 100 /*半径平方和的二次表达式*/ 101 a=1.0; b=0; c=0; 102 tmp = 0; 103 for(int i=2; i<=n; i++){ 104 a += 1.0; 105 tmp = d[i]-tmp; 106 c += tmp*tmp; 107 if(i%2 == 0) b -= 2.0*tmp; 108 else b += 2.0*tmp; 109 } 110 111 /* 112 错误地以为最低点为唯一取值点,若最低点不符合则无解. 113 r=(-b)/(2.0*a); 114 if(sign(r)<0) r=0; 115 flag = check(r); 116 */ 117 118 /*检查每条边计算三分时r的可行范围*/ 119 double low=0, high = d[1]; 120 tmp = 0; 121 for(int i=2; i<=n; i++){ 122 if(i%2 == 0){ 123 tmp += d[i]; 124 high = min(high, tmp); 125 } 126 else{ 127 tmp -= d[i]; 128 low = max(low, tmp); 129 } 130 } 131 132 if(low > high) flag = 0; 133 else{ 134 r = solve(low, high); 135 flag = check(r); 136 } 137 } 138 139 end: 140 if(!flag) printf("IMPOSSIBLE\n"); 141 else{ 142 double R[maxn]; 143 R[1]=r; 144 double temp = 0; 145 for(int i=2; i<=n; i++){ 146 temp = d[i]-R[i-1]; 147 R[i] = temp; 148 } 149 double ans = 0; 150 for(int i=1; i<=n; i++){ 151 //ans += R[i]*R[i]*PI;精度问题 152 ans += R[i]*R[i]; 153 } 154 155 printf("%.2lf\n", ans*PI); 156 for(int i=1; i<=n; i++){ 157 printf("%.2lf\n", R[i]); 158 } 159 } 160 161 } 162 163 return 0; 164 }
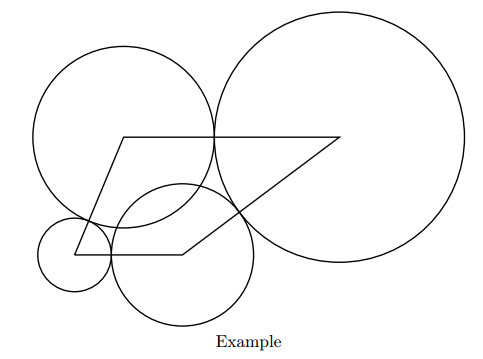
HDU 4791 Rebuild (2015长春现场赛,计算几何+三分)
标签:
原文地址:http://www.cnblogs.com/Sunshine-tcf/p/4940699.html