标签:
定义ai表示红色和绿色方块中方块数为偶数的颜色有i个,i = 0,1,2。
aij表示刷到第j个方块时的方案数,这是一个线性递推关系。
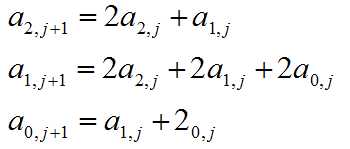
可以构造递推矩阵A,用矩阵快速幂求解。

1 /********************************************************* 2 * ------------------ * 3 * author AbyssalFish * 4 **********************************************************/ 5 #include<cstdio> 6 #include<iostream> 7 #include<string> 8 #include<cstring> 9 #include<queue> 10 #include<vector> 11 #include<stack> 12 #include<vector> 13 #include<map> 14 #include<set> 15 #include<algorithm> 16 #include<cmath> 17 using namespace std; 18 19 typedef long long ll; 20 21 #define PB push_back 22 const int maxn = 3, mod = 1e4+7; 23 const int n = 3; 24 typedef int MType; 25 typedef vector<MType> row; 26 typedef vector<row> mat; 27 struct Matrix 28 { 29 mat dat; 30 row &operator [](int x){ return dat[x]; } 31 Matrix operator * (Matrix& B) { 32 Matrix re; 33 re.dat.resize(n,row(3,0)); 34 for(int i = 0; i < n; i++){ 35 for(int j = 0; j < n; j++){ 36 for(int k = 0; k < n; k++){ 37 re[i][j] = (re[i][j]+dat[i][k]*B[k][j])%mod; 38 } 39 } 40 } 41 return re; 42 } 43 Matrix operator ^ (int q){ 44 Matrix Re, A = *this; 45 Re.dat.resize(n,row(3,0)); 46 for(int i = 0; i < n; i++) { 47 Re[i][i] = 1; 48 } 49 while(q){ 50 if(q&1){ 51 Re = Re * A; 52 } 53 A = A * A; 54 q >>= 1; 55 } 56 return Re; 57 } 58 }; 59 60 //#define LOCAL 61 int main() 62 { 63 #ifdef LOCAL 64 freopen("in.txt","r",stdin); 65 #endif 66 Matrix A; 67 A.dat.resize(3,row(3,0)); 68 A[0][0] = 2; A[0][1] = 1; 69 fill(A.dat[1].begin(),A.dat[1].end(),2); 70 A[2][1] = 1; A[2][2] = 2; 71 int T; scanf("%d",&T); 72 while(T--){ 73 int N; scanf("%d",&N); 74 //mat R = .dat;+R[0][1]+R[0][2] 75 printf("%d\n", (A^N)[0][0]); 76 } 77 return 0; 78 }
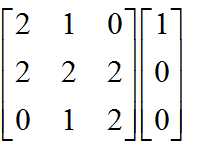
由初值可知,最后答案为Ak(1,1),复杂度是O(3^3*logN)。
如果利用特征值的话,效率会更高。
A的对角化矩阵Λ为
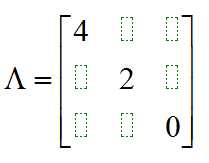
如果对应的特征向量矩阵为P,Ak = P * Λk * P‘。
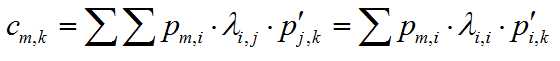
因为除了对角元都为0,所以可以去掉一个和号,而特征值4对应的系数为1/4,2对应的系数为1/2,因此最终答案为4n-1+2n-1。

1 /********************************************************* 2 * ------------------ * 3 * author AbyssalFish * 4 **********************************************************/ 5 #include<cstdio> 6 #include<iostream> 7 #include<string> 8 #include<cstring> 9 #include<queue> 10 #include<vector> 11 #include<stack> 12 #include<vector> 13 #include<map> 14 #include<set> 15 #include<algorithm> 16 #include<cmath> 17 using namespace std; 18 19 const int mod = 1e4+7; 20 int pow_mod(int a,int q) 21 { 22 int re = 1; 23 while(q){ 24 if(q&1) re = (re*a)%mod; 25 a = (a*a)%mod; 26 q>>=1; 27 } 28 return re; 29 } 30 //#define LOCAL 31 int main() 32 { 33 #ifdef LOCAL 34 freopen("in.txt","r",stdin); 35 #endif 36 int T; scanf("%d",&T); 37 while(T--){ 38 int N; scanf("%d",&N); 39 printf("%d\n",(pow_mod(4,N-1)+pow_mod(2,N-1))%mod); 40 } 41 return 0; 42 }
标签:
原文地址:http://www.cnblogs.com/jerryRey/p/4945587.html