标签:
由刚才的理论得知我们要求极点,来解出系统的振型看看有没有发散的部分。那么求极点的时候我们会有开环传递函数求极点和闭环传递函数求极点的问题,下面分开叙述。
对于一个已经知道闭环表达式的系统:
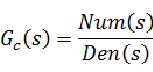
只要简单的令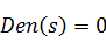 即可,但是题目经常给的是开环传递函数。
即可,但是题目经常给的是开环传递函数。
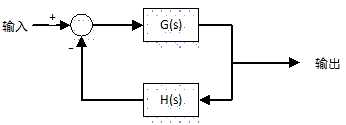
对于如上图所示的带反馈的系统,其闭环传递函数就是:
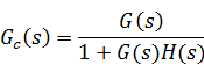
和上面一样,可以得到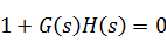 ,带进去就好了。
,带进去就好了。
但是如果给的是开环传递函数:
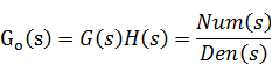
从上面得到的结论(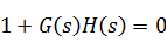 )可得:
)可得:
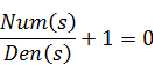
也就是说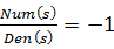 ,稍微推导可以得到:
,稍微推导可以得到: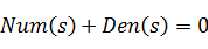
所以,不管是开环传递函数的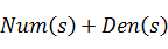 ,还是闭环传递函数的
,还是闭环传递函数的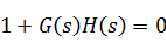 或者是
或者是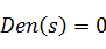 ,这个等式不妨叫他特征方程吧!
,这个等式不妨叫他特征方程吧!
最原始的思路:吧这个方程解出来就好了嘛!
假设特征方程是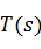 ,能把
,能把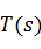 化成
化成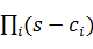 ,其中
,其中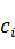 是复数,是方程的根,也就是系统的零极点了。
是复数,是方程的根,也就是系统的零极点了。
哪有这么好的事情啊,一般是解不出来的,超过五次就很难解了,应该说是不可解,但是高阶的系统的稳定性又不是不要判别,所以有如下方法:
比如,赫尔维茨判据:原理是特征方程的主行列式的顺序主子式全部是正的。
看着就很烦,所以一般使用劳斯表。
至于这两种方法的原理么……想不开的话就去看看吧……
假设我们得到的特征方程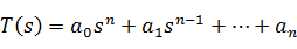 ,那么可以有表头:
,那么可以有表头:
|
|
| …… | …… |
|
| …… | …… |
|
如果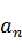 正好落在上面,那么下面补零:
正好落在上面,那么下面补零:
|
|
| …… |
|
|
| …… | …… |
|
下面一行的求法:
首先确定除法因子:左下角的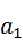 ,随后,第一个元素等于
,随后,第一个元素等于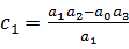 ,第二个元素是
,第二个元素是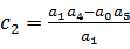 ,就是第一列和第n+1列拼成的行列式的负数值,然后除以左下角的数值。
,就是第一列和第n+1列拼成的行列式的负数值,然后除以左下角的数值。

上图是交叉相乘求下一行的示意图
不足的地方补零就好了,最后出现两个都是0的列就不要算了,因为算了也是0。可想而知,这样算一行就短一个,有的时候命好还能短2个,知道最后只剩一个就可以停了。
但是,如果算出来某一行第一个是0就日了狗了,那样下一行全是无穷大,大清要亡啊!
这个时候一般用把特征方程乘以一个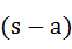 ,这里的a肯定得小于0啊,要不然加上这一项瞬间就肯定是发散了。
,这里的a肯定得小于0啊,要不然加上这一项瞬间就肯定是发散了。
还有一种情况,还没算完呢,已经全部是0了,这不能停啊。
劳斯说,这种情况是因为方程里有绝对值一样大但是符号相反的特征根,比如纯虚的共轭复述根,对称于实轴的两对共轭复根什么的,姑且相信他吧!
个人认为出现这种情况直接可以判断为不稳定了。
假设全零行上面一行是:
|
| …… | …… |
|
那么可以设立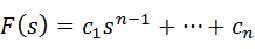 ,得到
,得到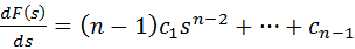
那么用
|
| …… | …… |
|
代替全零行即可。
劳斯判据:得到的表的第一列现在没有0了,如果也没有小于0的数字,那么就是稳定的,否则不稳定。
而且第一列的符号改变的次数就是实部大于0的根的数目。
标签:
原文地址:http://www.cnblogs.com/TsingJyujing/p/4945947.html