标签:
贝叶斯定理:
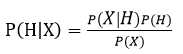
X是已知条件,H是假设。映射到文本分类中,X就是给定的测试文档,H是文档属于的类别。
朴素贝叶斯分类:
即求出所有类的P(Ci|X),概率最大的类为预测类。
因为P(X)是一样的,只需求P(X|C)P(C)即可。
(1)P(Ci)=Ci类文档数/训练文档集总文档数
(2)P(X|Ci)不好求,因此需要“朴素”的假设:类条件独立,即属性值相互独立,则
P(X|Ci)=P(x1|Ci)P(x2|Ci)...P(xn|Ci) xi为文档的各个属性,即特征词
<1>把x当离散型属性,即只有包含/不包含两种情况,则P(xk|Ci)=(Ci类中包含特征词xk的文本数+1)/Ci类总文本数
<2>记得使用经典TF-IDF公式可以对每个文档内的特征词计算其权重,这时候x就是连续值属性了。
对于连续值属性,一般假定服从均值μ,标准差σ的高斯分布
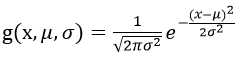
因此P(xk|Ci)=g(xk,μCi,σCi)
看上去很复杂,其实μCi是Ci类内特征词t的权值的均值,σCi是标准差
对于一个测试文档,使用TF-IDF计算特征词权值,即得到xk,三个参数一起代入公式可得P(xk|Ci)
求得每个类P(X|Ci)后,P最大的类为预测类。
标签:
原文地址:http://www.cnblogs.com/IvanSSSS/p/4946983.html