Knight's Trip---hdu3766（马走日求最小走的步数）

/**
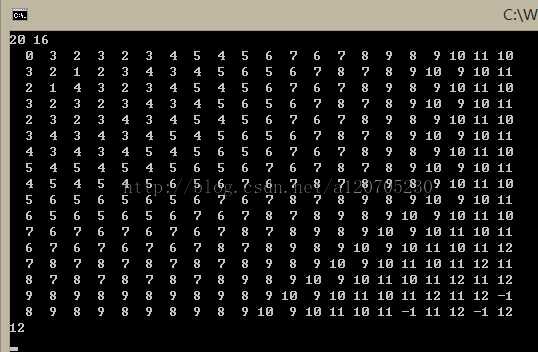
首先，xy的大小排序和转化为都是正数步数不变应该懂吧。
y=2*x这种情况直接就是(x+y)/3步。
如果y<2*x但是（x+y）%3==0的话，那么我们可以通过控制（1,2），（2,1）
两种跳法的次数达到...总数必然是(x+y)/3，然后xy的和对3取余是1的话，
我们是不是必然可以在(x+y-1)/3步的时候跳到(x,y-1)这个点，但是不能一步
跳到(x,y)，回撤两步到(x-4,y-5)这个点，我们可以用三步跳到(x,y)，那么
就是原先的步数+1。余数为2，就是先跳到(x-1,y-1)这个地方，我们知道(0,0)
到(1,1)只需要两步，那么(x-1,y-1)到(x,y)也就是原先步数+2.然后考虑y>2*x，
先把(0,1)的情况特殊处理一下。接着我们可以用x步跳到(x,y)，那么原问题就
转化为(0,0)到(0,y-2*x)。当y-2*x是4的倍数的话我们可以直接(1,2)(-1,2)这个
跳可以在(y-2*x)/2步到达。余数为1，就是(0,0)到(0,1)的问题，但是这个需要
三步不是最优的，我们后撤两步变为(0,0)到(0,5)，我们可以三步达到，那么就
是原先的步数加上1就是解。余数为2，我们可以分别跳一次(2,1)(-2,1)到达。
余数为3，转化为(0,0)到(0,3）的问题我们可以(-1,2)(1,1)(0,3)三步到达。
以上就是全部情况，o(╯□╰)o，在纸上画画，应该所有在这这几类范围内。
**/
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
#define N 20100

int main()
{
    int x, y, ans;
    char s[110];
    while(scanf("%s", s), strcmp(s, "END"))
    {
        sscanf(s, "%d", &x);
        scanf("%d", &y);
        x=abs(x);
        y=abs(y);
        if(x>y)swap(x, y);

        if(y==x*2)
        {
            printf("%d\n", (x+y)/3);
            continue;
        }
        if(y<=2*x)
        {
            if(x==1&&y==1)
                ans = 2;
            else if(x==2&&y==2)
                ans = 4;
            else
                ans = (x+y)/3+(x+y)%3;
        }
        else
        {
            ans=x;
            int c=(y-2*x)%4;
            ans+=c;
            ans+=(y-2*x-c)/2;
            if(y==1&&x==0)
                ans=3;
        }
        printf("%d\n",ans);
    }
    return 0;
}