标签:
As you know, an undirected connected graph with n nodes and n - 1 edges is called a tree. You are given an integer d and a tree consisting of n nodes. Each node i has a value ai associated with it.
We call a set S of tree nodes valid if following conditions are satisfied:
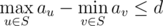 .
.Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo 1000000007(109 + 7).
The first line contains two space-separated integers d (0 ≤ d ≤ 2000) and n (1 ≤ n ≤ 2000).
The second line contains n space-separated positive integers a1, a2, ..., an(1 ≤ ai ≤ 2000).
Then the next n - 1 line each contain pair of integers u and v (1 ≤ u, v ≤ n) denoting that there is an edge between u and v. It is guaranteed that these edges form a tree.
Print the number of valid sets modulo 1000000007.
1 4
2 1 3 2
1 2
1 3
3 4
8
In the first sample, there are exactly 8 valid sets: {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {3, 4} and {1, 3, 4}. Set {1, 2, 3, 4} is not valid, because the third condition isn‘t satisfied. Set {1, 4} satisfies the third condition, but conflicts with the second condition.
题意:给你一个n点的树,和每个点的权值,问你多少种子树满足(最大权值点-最小权值点)<=d
题解:定义dp[i]表示以i为最小权值根节点的子树方案数,注意维护此条件
于是答案就是 ∑dp[i] %mod (1<=i<=n);

///1085422276 #include<bits/stdc++.h> using namespace std ; typedef long long ll; #define mem(a) memset(a,0,sizeof(a)) #define pb push_back #define meminf(a) memset(a,127,sizeof(a)); inline ll read() { ll x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){ if(ch==‘-‘)f=-1;ch=getchar(); } while(ch>=‘0‘&&ch<=‘9‘){ x=x*10+ch-‘0‘;ch=getchar(); }return x*f; } //**************************************** #define maxn 2000+50 #define mod 1000000007 #define inf 1000000007 int d,n,a[maxn],vis[maxn]; vector<int >G[maxn]; ll dp[maxn];//以i为最小根节点,的方案数 void dfs(int x,int pre){ dp[x]=1;vis[x]=1; for(int i=0;i<G[x].size();i++){ if(!vis[G[x][i]]){ if(a[G[x][i]]<a[pre]||a[G[x][i]]>a[pre]+d)continue; if(a[G[x][i]]==a[pre]&&G[x][i]<pre)continue; dfs(G[x][i],pre); dp[x]=(dp[x]*(dp[G[x][i]]+1))%mod; } } } int main(){ d=read(),n=read(); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); }int u,v; for(int i=1;i<n;i++){ scanf("%d%d",&u,&v); G[u].pb(v);G[v].pb(u); }ll ans=0; for(int i=1;i<=n;i++){ mem(dp);mem(vis); dfs(i,i); ans=(ans+dp[i])%mod; } cout<<ans<<endl; return 0; }
Codeforces Round #277 (Div. 2) D. Valid Sets DP
标签:
原文地址:http://www.cnblogs.com/zxhl/p/4948753.html